5172⭐ is a 5-digit number. If the number is divisible by 6, find all the possible values of ⭐.

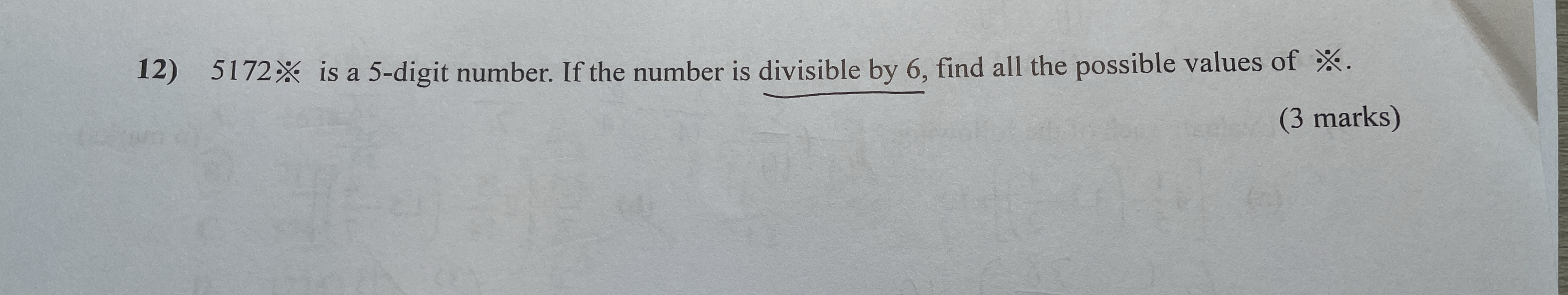
Understand the Problem

The question is asking to find all possible values for the digit represented by '⭐' in the number 5172⭐, given that the entire 5-digit number must be divisible by 6. To determine divisibility by 6, the number must be divisible by both 2 and 3.

Answer

The possible values for '⭐' are 0 and 6.

Steps to Solve

Check Divisibility by 2

For a number to be divisible by 2, its last digit must be even. Therefore, the digit represented by '⭐' must be one of the even digits: 0, 2, 4, 6, or 8.

Check Divisibility by 3

To determine divisibility by 3, the sum of the digits of the number must be divisible by 3. The digits in our number are 5, 1, 7, 2, and '⭐'.

First, calculate the sum of the known digits: $$ 5 + 1 + 7 + 2 = 15 $$

Now, include '⭐': $$ 15 + ⭐ $$

Set Up the Divisibility Condition

For the total sum $15 + ⭐$ to be divisible by 3, we can analyze this for each of the even candidates for '⭐':

If '⭐' = 0: $15 + 0 = 15$ (divisible by 3)
If '⭐' = 2: $15 + 2 = 17$ (not divisible by 3)
If '⭐' = 4: $15 + 4 = 19$ (not divisible by 3)
If '⭐' = 6: $15 + 6 = 21$ (divisible by 3)
If '⭐' = 8: $15 + 8 = 23$ (not divisible by 3)

Conclusion of Possible Values

The digits for '⭐' that make the entire number divisible by both 2 and 3 are 0 and 6.

The possible values for '⭐' are 0 and 6.

More Information

A number is divisible by 6 if it meets the conditions for divisibility by both 2 and 3. In this case, the even digits are essential for the number to be divisible by 2, while the sum of the digits must meet the criteria for divisibility by 3.

Tips

Forgetting to check both conditions for divisibility by 2 and 3.
Miscalculating the sum of the digits including '⭐'.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!