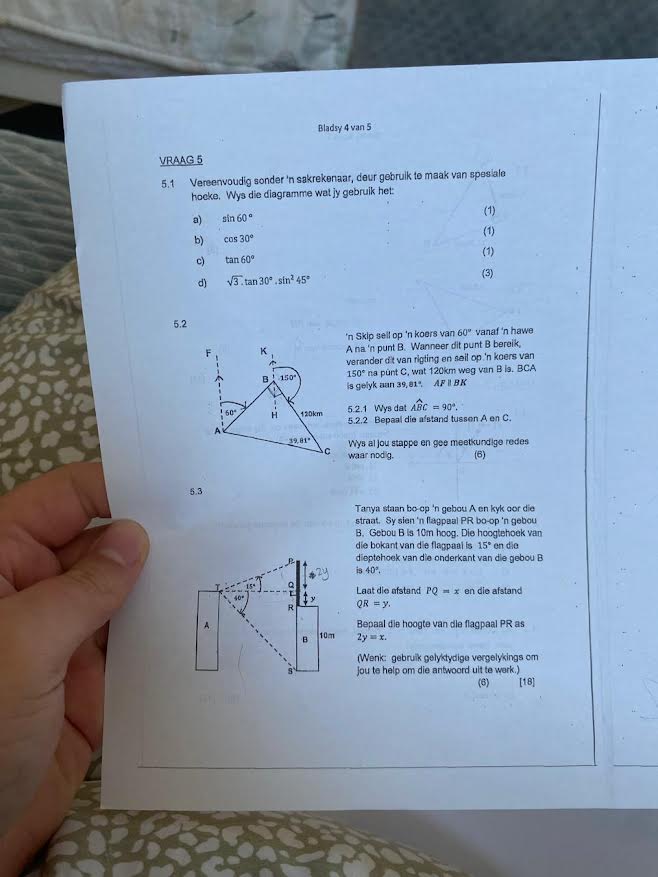
5.1 Vereenvoudig sonder 'n sakrekenaar, deur gebruik te maak van spesiale hoeke. Wys die diagramme wat jy gebruik het: a) sin 60° b) cos 30° c) tan 60° d) √3 tan 30° sin 45° 5.2 'n... 5.1 Vereenvoudig sonder 'n sakrekenaar, deur gebruik te maak van spesiale hoeke. Wys die diagramme wat jy gebruik het: a) sin 60° b) cos 30° c) tan 60° d) √3 tan 30° sin 45° 5.2 'n Skip seel op 'n koers van 60° vanaf A na punt B. Wanneer dit punt B bereik, verander dit na 'n ligging en seil op 'n koers van 150° na punt C, wat 120km weg van B is. BCA is gelyk aan 39°. 5.2.1 Wys dat ∠ABC = 90°. 5.2.2 Bepaal die afstand tussen A en C. 5.3 Tanyas staan bo-op 'n gebou A en kyk oor die straat. Sy sien 'n vlagpal PR bo-op die gebou B. Gebou B is 10m hoog. Die hoogtepunt van die bokant van die vlagpal is 15° en die dieptehoek van die onderste kant van die gebou B is 40°. Laat die afstand PQ = x en die afstand QR = y. Bepaal die hoogte van die vlagpal PR as 2y = y.
Understand the Problem
Die vraag vra vir die verduideliking van spesifieke diagramme en rekene probleme wat verband hou met trigonometrie, spesifiek met betrekking tot spesiale hoeke en die toepassing daarvan in 'n driehoek en 'n gebou.
Answer
Die oplossings is: - 5.1 a) $\frac{\sqrt{3}}{2}$, b) $\frac{\sqrt{3}}{2}$, c) $\sqrt{3}$, d) $\frac{1}{\sqrt{2}}$. - 5.3 se finale hoogte sal afhanklik wees van die gevonde afstand QR en die berekeningen.
Answer for screen readers
Die antwoorden vir 5.1 is:
- a) $\frac{\sqrt{3}}{2}$
- b) $\frac{\sqrt{3}}{2}$
- c) $\sqrt{3}$
- d) $\frac{1}{\sqrt{2}}$
Afstand tussen A en C vir 5.2.2 kan gevind word deur die toepaslike waardes in te vul. Die finale hoogte vir 5.3 moet die vyf berekeninge insluit.
Steps to Solve
- Oplossing vir 5.1 a - d
Hier is die spesiale hoeke wat gebruik kan word om die waardes te bereken.
- a) $\sin 60^\circ = \frac{\sqrt{3}}{2}$
- b) $\cos 30^\circ = \frac{\sqrt{3}}{2}$
- c) $\tan 60^\circ = \sqrt{3}$
- d) $\sqrt{3} \cdot \tan 30^\circ \cdot \sin 45^\circ = \sqrt{3} \cdot \frac{1}{\sqrt{3}} \cdot \frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}}$
- Oplossing vir 5.2.1
In driehoek ABC, met die hoeke gegee as:
- $\angle A = 60^\circ$
- $\angle B = 90^\circ$
- $\angle C = 30^\circ$
Gebruik die som van die hoeke in 'n driehoek: $$ \angle A + \angle B + \angle C = 180^\circ $$
- Oplossing vir 5.2.2
Om die afstand tussen A en C te bepaal, kan ons die sinus en kosinus funksies gebruik:
- In driehoek $ABK$: $AB = 120\ \text{m}$, $\angle ABC = 60^\circ$
$$ AC = \frac{AB}{\sin(\angle B)} $$
Hier kan jy die waardes invul.
- Oplossing vir 5.3
Maak gebruik van die gegewe data:
- Gebou A is 10 m hoog.
- Gebou B hoogte = 2y m.
- Die hoek van die vlagnys PR is 15°.
Gebruik die tangens om die hoogte van B te vind: $$ \tan(15^{\circ}) = \frac{\text{hoogte B}}{QR} = \frac{2y}{QR} $$
- Finale hoogte met insluiting van afstand
Oorweeg die afstand $\overline{PQ}$, volgens die tangens van die hoeke wat betrokke is om die hooftoetsafstand QR te verkrijg: $$ PQ = QR + AB = QR + 10 \ \text{m} $$
Die antwoorden vir 5.1 is:
- a) $\frac{\sqrt{3}}{2}$
- b) $\frac{\sqrt{3}}{2}$
- c) $\sqrt{3}$
- d) $\frac{1}{\sqrt{2}}$
Afstand tussen A en C vir 5.2.2 kan gevind word deur die toepaslike waardes in te vul. Die finale hoogte vir 5.3 moet die vyf berekeninge insluit.
More Information
Die gebruik van spesiale hoeke is belangrik in trigonometrie, aangesien dit 'n vinnige manier bied om trigonometriese funksies te bereken, wat handig is in toegepaste probleme soos diegene in die diagram.
Tips
- Verkeerde gebruik van die trigonometriese funksies; maak seker dat jy die korrekte hoeke vir die spesifieke driehoekekies gebruik.
- Vergeten om die eenhede aan te dui en korrek te verwerk in die finale antwoord.
AI-generated content may contain errors. Please verify critical information