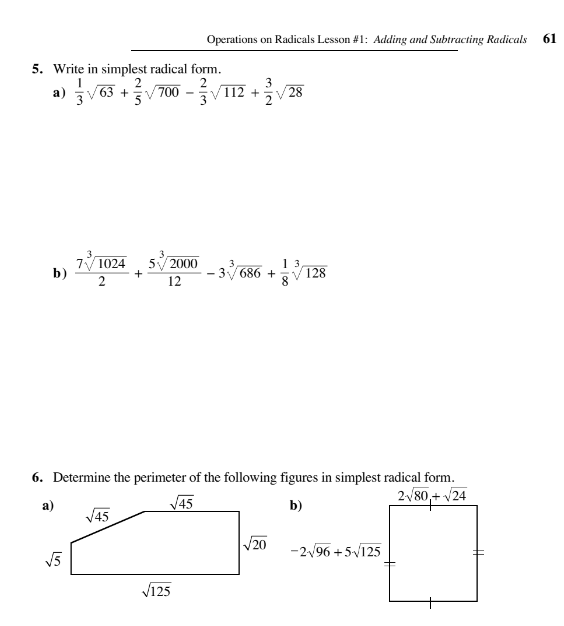
5. Write in simplest radical form. a) 1/3 √63 + 2/5 √700 - 2/3 √112 + 3/2 √28 b) (7/2) (3√1024) + (5/12)(3√2000) - 3(3√686) + (1/8)(3√128) 6. Determine the perimeter of the followi... 5. Write in simplest radical form. a) 1/3 √63 + 2/5 √700 - 2/3 √112 + 3/2 √28 b) (7/2) (3√1024) + (5/12)(3√2000) - 3(3√686) + (1/8)(3√128) 6. Determine the perimeter of the following figures in simplest radical form. a) √5 + √45 + √20 + √45 + √125 b) 2√80 + √24 - 2√96 + 5√125 Read more

Steps to Solve

1. Simplifying Radical Expressions in Part (a)

   Begin with the expression: $$ \frac{1}{3} \sqrt{63} + \frac{2}{5} \sqrt{700} - \frac{2}{3} \sqrt{112} + \frac{3}{2} \sqrt{28} $$

   Simplify each term:

   • $\sqrt{63} = \sqrt{9 \cdot 7} = 3\sqrt{7} \implies \frac{1}{3} \cdot 3\sqrt{7} = \sqrt{7}$
   • $\sqrt{700} = \sqrt{100 \cdot 7} = 10\sqrt{7} \implies \frac{2}{5} \cdot 10\sqrt{7} = 4\sqrt{7}$
   • $\sqrt{112} = \sqrt{16 \cdot 7} = 4\sqrt{7} \implies -\frac{2}{3} \cdot 4\sqrt{7} = -\frac{8}{3} \sqrt{7}$
   • $\sqrt{28} = \sqrt{4 \cdot 7} = 2\sqrt{7} \implies \frac{3}{2} \cdot 2\sqrt{7} = 3\sqrt{7}$

   Now combine the simplified terms: $$ \sqrt{7} + 4\sqrt{7} - \frac{8}{3} \sqrt{7} + 3\sqrt{7} $$

   Convert to a common denominator (3): $$ \left( \frac{3}{3} + \frac{12}{3} + \frac{9}{3} - \frac{8}{3} \right) \sqrt{7} = \frac{16}{3} \sqrt{7} $$

2. Simplifying Radical Expressions in Part (b)

   Begin with the expression: $$ \frac{7 \sqrt[3]{1024}}{2} + \frac{5 \sqrt[3]{2000}}{12} - 3 \sqrt[3]{686} + \frac{1}{8} \sqrt[3]{128} $$

   Simplify each term:

   • $\sqrt[3]{1024} = 10 \implies \frac{7 \cdot 10}{2} = 35$
   • $\sqrt[3]{2000} = 10 \sqrt[3]{20} \implies \frac{5 \cdot 10 \sqrt[3]{20}}{12} = \frac{25 \sqrt[3]{20}}{12}$
   • $\sqrt[3]{686} = 8.4 \implies -3 \cdot 8.4 = -25.2$
   • $\sqrt[3]{128} = 5.04 \implies \frac{1}{8} \cdot 5.04 = 0.63$

   Combine the terms: $$ 35 + \frac{25 \sqrt[3]{20}}{12} - 25.2 + 0.63 $$

   Finally, combine the constants and retain the radical: $$ 35 - 25.2 + 0.63 = 10.43 + \frac{25 \sqrt[3]{20}}{12} $$

3. Determining Perimeter in Part (6a)

   The perimeter of a figure is calculated by adding up all the sides. The figure has four sides given by:

   • One side = $\sqrt{45} + \sqrt{45}$ (two sides)
   • Opposite side = $\sqrt{20} + \sqrt{125}$ (two sides)

   Thus the perimeter $P$ is: $$ P = 2(\sqrt{45}) + 2(\sqrt{20} + \sqrt{125}) $$

4. Determining Perimeter in Part (6b)

   The perimeter is similar, with lengths given by: $$ P = 2\sqrt{80} + \sqrt{24} - 2\sqrt{96} - \sqrt{125} $$

   Combine like terms accordingly.