5 - 2(3 - x) = 4x + 10
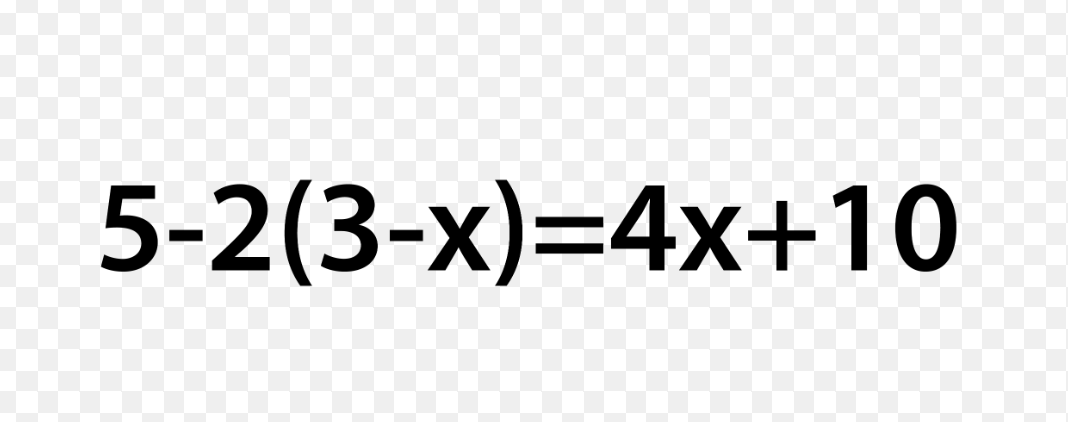
Understand the Problem
The question presents an algebraic equation that needs to be solved for the variable x. The equation involves distribution and combining like terms before isolating x.
Answer
The solution is $x = -\frac{11}{2}$.
Answer for screen readers
The value of $x$ is $-\frac{11}{2}$.
Steps to Solve
- Distribute the -2
First, apply the distributive property to the left side of the equation: $$ 5 - 2(3 - x) = 5 - 6 + 2x $$
- Combine like terms on the left side
Combine the constants on the left side: $$ 5 - 6 + 2x = -1 + 2x $$
Now the equation looks like this: $$ -1 + 2x = 4x + 10 $$
- Rearrange the equation
To isolate $x$, move $2x$ to the right side by subtracting $2x$ from both sides: $$ -1 = 4x - 2x + 10 $$
This simplifies to: $$ -1 = 2x + 10 $$
- Isolate the variable x
Now, subtract 10 from both sides to isolate terms with $x$: $$ -1 - 10 = 2x $$ $$ -11 = 2x $$
- Solve for x
Finally, divide both sides by 2 to solve for $x$: $$ x = -\frac{11}{2} $$
The value of $x$ is $-\frac{11}{2}$.
More Information
This is a linear equation in one variable. The solution indicates that $x$ can take negative values, emphasizing that solutions can exist below zero.
Tips
- Forgetting to distribute correctly can lead to errors; always ensure to multiply all terms inside the parentheses.
- Miscombining like terms can result in incorrect coefficients; check carefully.
AI-generated content may contain errors. Please verify critical information