(4x + 1)(3x - 7) - (3x - 4)(2x + 8)

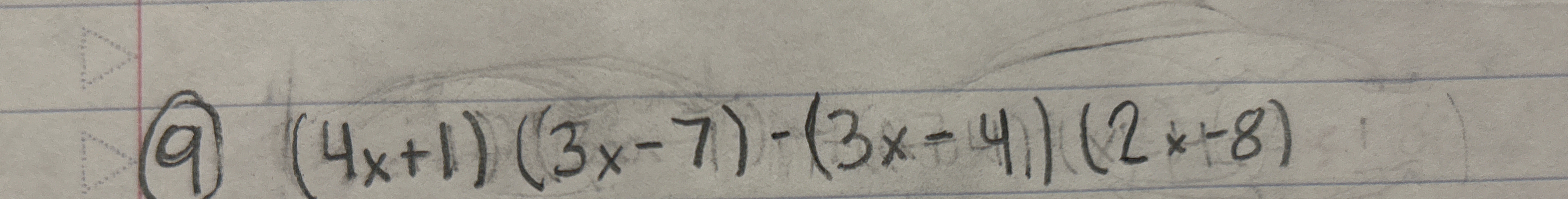
Understand the Problem

The question is asking us to simplify or solve an expression involving multiple polynomial terms. We need to carry out the operations indicated in the expression step by step.

Answer

The simplified expression is $ 6x^2 - 41x + 25 $.

Steps to Solve

Expand the First Set of Parentheses

First, we need to distribute the terms in the expression $(4x + 1)(3x - 7)$:

[ (4x + 1)(3x - 7) = 4x \cdot 3x + 4x \cdot (-7) + 1 \cdot 3x + 1 \cdot (-7) ]

Calculating each term gives us:

[ = 12x^2 - 28x + 3x - 7 ]

Combining like terms results in:

[ = 12x^2 - 25x - 7 ]

Expand the Second Set of Parentheses

Next, we expand the expression $(3x - 4)(2x + 8)$:

[ (3x - 4)(2x + 8) = 3x \cdot 2x + 3x \cdot 8 + (-4) \cdot 2x + (-4) \cdot 8 ]

Calculating each term gives us:

[ = 6x^2 + 24x - 8x - 32 ]

Combining like terms results in:

[ = 6x^2 + 16x - 32 ]

Combine Both Expressions

Now we can put everything together:

[ (12x^2 - 25x - 7) - (6x^2 + 16x - 32) ]

This equates to:

[ 12x^2 - 25x - 7 - 6x^2 - 16x + 32 ]

Combine Like Terms

Combining the like terms results in:

[ (12x^2 - 6x^2) + (-25x - 16x) + (-7 + 32) ]

Which simplifies to:

[ 6x^2 - 41x + 25 ]

The simplified expression is ( 6x^2 - 41x + 25 ).

More Information

This expression represents a quadratic polynomial. Quadratics are commonly used in various mathematical contexts, such as solving for vertex points, axis of symmetry, and can be applied in real-world problems involving projectile motion.

Tips

Forgetting to distribute correctly: Ensure that each term in the first parentheses is multiplied by each term in the second parentheses.
Neglecting to combine like terms correctly: After expansion, remember to combine the coefficients of similar polynomial terms.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!