4 + 4v ≥ -8
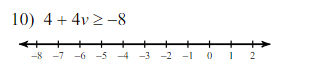
Understand the Problem
The question is asking to solve the inequality 4 + 4v ≥ -8 and represent the solution on a number line. To solve it, we will isolate the variable v and then depict the solution graphically.
Answer
The solution is $v \geq -3$.
Answer for screen readers
The solution to the inequality is $v \geq -3$.
Steps to Solve
-
Isolate the variable term To begin solving the inequality $4 + 4v \geq -8$, we will first subtract 4 from both sides of the inequality: $$ 4v \geq -8 - 4 $$ This simplifies to: $$ 4v \geq -12 $$
-
Divide by the coefficient of v Next, we divide both sides of the inequality by 4 to isolate $v$: $$ v \geq \frac{-12}{4} $$ This simplifies to: $$ v \geq -3 $$
-
Graph the solution on a number line To represent the solution $v \geq -3$ on a number line, we place a solid dot on the point -3 (indicating that -3 is included in the solution) and shade to the right, since all numbers greater than -3 are part of the solution.
The solution to the inequality is $v \geq -3$.
More Information
This inequality indicates that $v$ can take any value greater than or equal to -3. Graphically, this means all numbers to the right of -3 are included in the solution set.
Tips
- Misinterpreting the inequality direction: Some may accidentally flip the inequality when dividing by a negative number (though it does not apply here since 4 is positive). Always remember that this only occurs when multiplying or dividing both sides by a negative number.
- Ignoring the inequality symbol: Ensure to correctly carry the inequality symbol through the process of solving.
AI-generated content may contain errors. Please verify critical information