(3x-1)² - (x+6)²

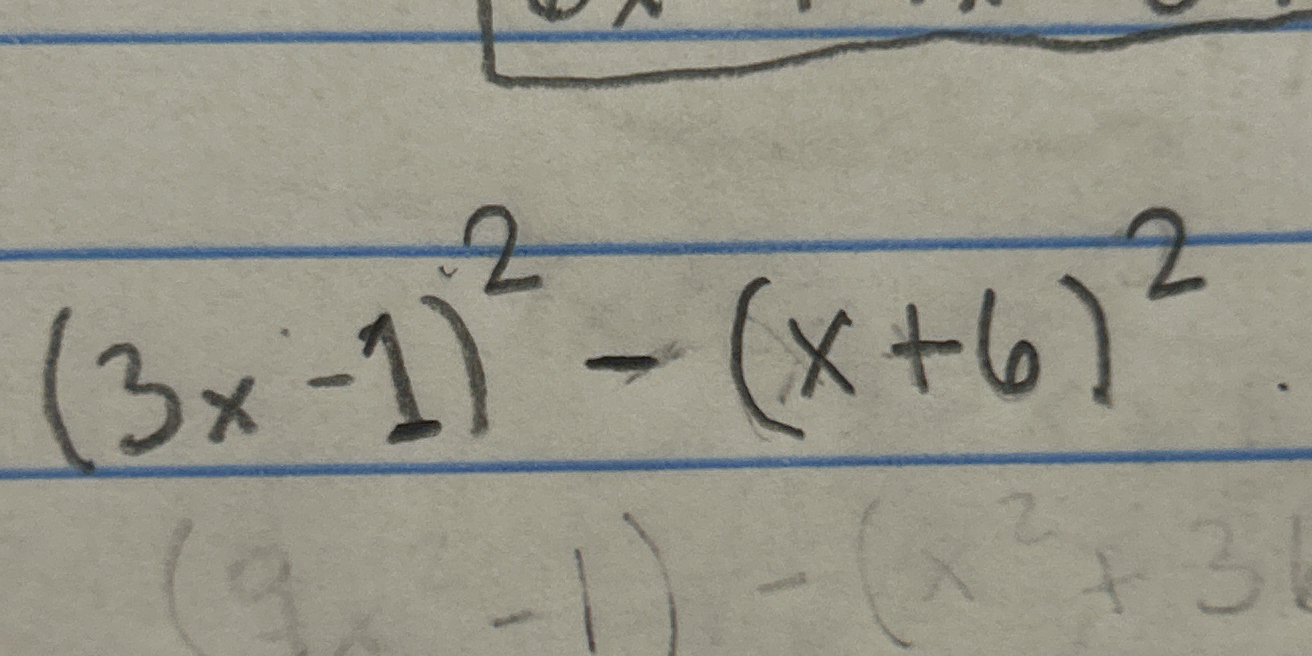
Understand the Problem

The question is asking for the simplification or evaluation of the expression (3x-1)² - (x+6)². This requires applying algebraic principles such as expansion and simplification.

Answer

The simplified expression is $8x^2 - 18x - 35$.

Steps to Solve

Expand the first square To expand $(3x - 1)^2$, use the formula $(a - b)^2 = a^2 - 2ab + b^2$: [ (3x - 1)^2 = (3x)^2 - 2(3x)(1) + (1)^2 = 9x^2 - 6x + 1 ]
Expand the second square Next, expand $(x + 6)^2$ using the formula $(a + b)^2 = a^2 + 2ab + b^2$: [ (x + 6)^2 = x^2 + 2(x)(6) + (6)^2 = x^2 + 12x + 36 ]
Subtract the second expansion from the first Now subtract the expansion of the second square from the first: [ (9x^2 - 6x + 1) - (x^2 + 12x + 36) ]
Combine like terms Distributing the negative sign and combining like terms: [ 9x^2 - 6x + 1 - x^2 - 12x - 36 = (9x^2 - x^2) + (-6x - 12x) + (1 - 36) ] This simplifies to: [ 8x^2 - 18x - 35 ]

The simplified expression is (8x^2 - 18x - 35).

More Information

The expression simplifies using the difference of squares and polynomial expansion. This is a common technique in algebra, often used in quadratic expressions.

Tips

Forgetting to square each term correctly when expanding.
Not distributing the negative sign when subtracting the second square.
Combining like terms incorrectly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!