(3x - 1)² - (x + 6)²
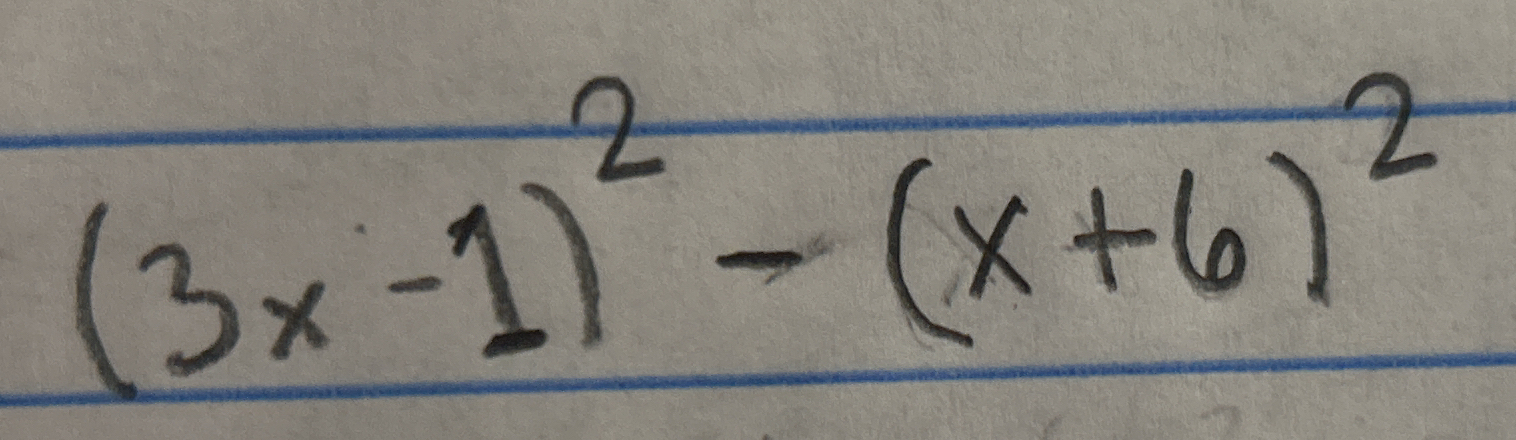
Understand the Problem
The question presents a mathematical expression involving square terms, specifically (3x - 1)² - (x + 6)². The goal is likely to simplify or evaluate this expression.
Answer
The simplified expression is $$ 8x^2 - 18x - 35 $$.
Answer for screen readers
The simplified expression is $$ 8x^2 - 18x - 35 $$.
Steps to Solve
- Expand the first square term
Using the formula $(a - b)^2 = a^2 - 2ab + b^2$, for $(3x - 1)^2$:
- Let $a = 3x$ and $b = 1$.
- We get:
$$ (3x - 1)^2 = (3x)^2 - 2(3x)(1) + 1^2 = 9x^2 - 6x + 1 $$
- Expand the second square term
For $(x + 6)^2$, we use the formula $(a + b)^2 = a^2 + 2ab + b^2$:
- Let $a = x$ and $b = 6$.
- We get:
$$ (x + 6)^2 = x^2 + 2(x)(6) + 6^2 = x^2 + 12x + 36 $$
- Combine the expanded expressions
Now substitute the expansions back into the original expression:
$$ (3x - 1)^2 - (x + 6)^2 $$
This gives:
$$ (9x^2 - 6x + 1) - (x^2 + 12x + 36) $$
- Simplify the expression
Combine like terms:
- First, distribute the negative sign:
$$ 9x^2 - 6x + 1 - x^2 - 12x - 36 $$
Combine similar terms:
$$ (9x^2 - x^2) + (-6x - 12x) + (1 - 36) = 8x^2 - 18x - 35 $$
The simplified expression is $$ 8x^2 - 18x - 35 $$.
More Information
This expression is the result of applying the difference of squares formula by expanding both square terms and combining like terms. Such expressions often arise in algebra, and simplifying them is a fundamental skill.
Tips
- Errors in expansion: Failing to properly apply the square formulas can lead to incorrect contributions of each term.
- Losing track of signs: Pay attention when distributing a negative sign during subtraction, as it can change the sign of all subsequent terms.
AI-generated content may contain errors. Please verify critical information