3 + p/4 > 2
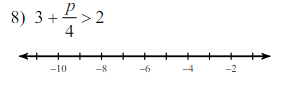
Understand the Problem
The question is asking us to solve the inequality 3 + (p/4) > 2 and then represent the solution on a number line.
Answer
The solution is \( p > -4 \).
Answer for screen readers
The solution to the inequality is ( p > -4 ).
Steps to Solve
- Isolate the term with ( p )
We start by subtracting 3 from both sides of the inequality to isolate the term with ( p ):
$$ 3 + \frac{p}{4} > 2 $$
becomes
$$ \frac{p}{4} > 2 - 3 $$
which simplifies to
$$ \frac{p}{4} > -1 $$
- Eliminate the fraction
Next, we multiply both sides of the inequality by 4 to eliminate the fraction. Remember that multiplying by a positive number does not change the direction of the inequality:
$$ p > 4 \times (-1) $$
This simplifies to:
$$ p > -4 $$
- Represent on a number line
To represent the solution ( p > -4 ) on a number line, we draw an open circle at -4 (indicating that -4 is not included in the solution) and shade to the right to indicate all numbers greater than -4.
The solution to the inequality is ( p > -4 ).
More Information
The solution ( p > -4 ) indicates that ( p ) takes on any value greater than -4. This is an example of a linear inequality, which can have infinitely many solutions represented on a number line.
Tips
- Not reversing the inequality: When multiplying or dividing by a negative number, the inequality sign should be reversed. In this case, we only multiplied by a positive number, so this mistake wasn’t applicable.
- Misreading the number line representation: It's important to remember that an open circle means the number is not included in the solution.
AI-generated content may contain errors. Please verify critical information