-(2x - 1)^2 + x > 0
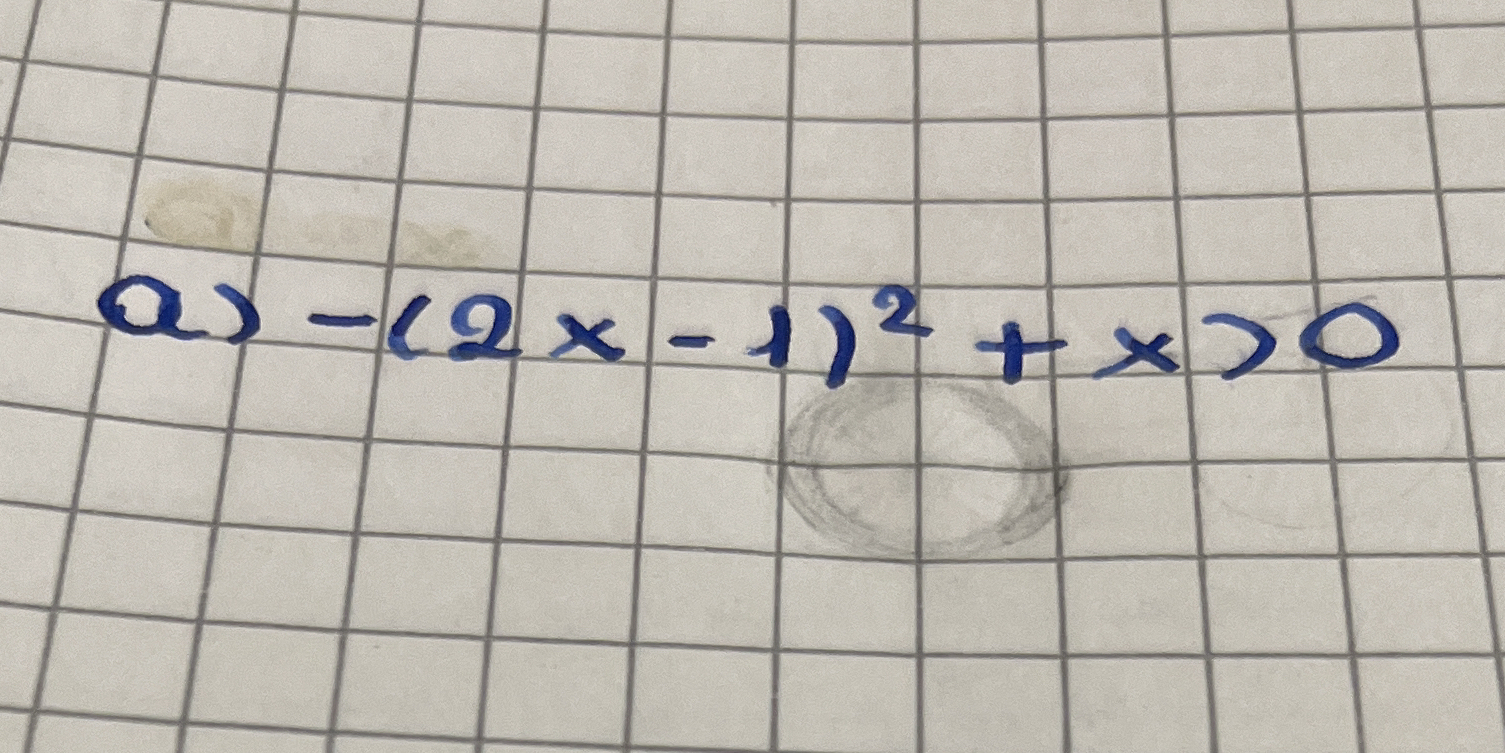
Understand the Problem
The question is asking to solve the inequality
- (2x - 1)^2 + x > 0. This involves manipulating the inequality to find the values of x that satisfy it.
Answer
$$ x < \frac{1}{4} \quad \text{or} \quad x > 1 $$
Answer for screen readers
The solution to the inequality is: $$ x < \frac{1}{4} \quad \text{or} \quad x > 1 $$
Steps to Solve
-
Rearrange the Inequality To simplify the inequality, we can start by moving everything to one side: $$ -(2x - 1)^2 + x > 0 $$ becomes $$ x - (2x - 1)^2 > 0 $$
-
Expand the Squared Term Next, we expand the squared term $-(2x - 1)^2$: $$ (2x - 1)^2 = 4x^2 - 4x + 1 $$ So we rewrite the inequality as: $$ x - (4x^2 - 4x + 1) > 0 $$ This simplifies to: $$ x - 4x^2 + 4x - 1 > 0 $$ Which further combines to: $$ -4x^2 + 5x - 1 > 0 $$
-
Factor the Quadratic Now, we need to factor the quadratic inequality: $$ -4x^2 + 5x - 1 > 0 $$ We can factor out $-1$ to make it easier: $$ 4x^2 - 5x + 1 < 0 $$ Next, we use the quadratic formula to find the roots: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ with $a = 4, b = -5, c = 1$: $$ x = \frac{5 \pm \sqrt{(-5)^2 - 4 \cdot 4 \cdot 1}}{2 \cdot 4} $$ $$ x = \frac{5 \pm \sqrt{25 - 16}}{8} $$ $$ x = \frac{5 \pm 3}{8} $$
-
Calculate the Roots Calculating the two roots gives: $$ x = \frac{5 + 3}{8} = 1 \quad \text{and} \quad x = \frac{5 - 3}{8} = \frac{1}{4} $$
-
Test Intervals Now we test the intervals defined by the roots: $(-\infty, \frac{1}{4}), (\frac{1}{4}, 1), (1, \infty)$.
- Pick $x = 0$: $$ 4(0)^2 - 5(0) + 1 = 1 > 0 $$
- Pick $x = 0.5$: $$ 4(0.5)^2 - 5(0.5) + 1 = 1 - 2.5 + 1 = -0.5 < 0 $$
- Pick $x = 2$: $$ 4(2)^2 - 5(2) + 1 = 16 - 10 + 1 = 7 > 0 $$
Thus, the inequality holds for the intervals $(-\infty, \frac{1}{4})$ and $(1, \infty)$.
The solution to the inequality is: $$ x < \frac{1}{4} \quad \text{or} \quad x > 1 $$
More Information
This inequality shows that the values of $x$ that make the expression negative can be found outside the interval defined by the roots (\frac{1}{4}) and (1).
Tips
- Incorrect Expansion: Ensure you expand the squared term correctly.
- Ignoring the Negative Sign: Remember that when moving from ( -(A) > 0 ) to ( A < 0 ), the order of the inequality flips when multiplying or dividing by a negative number.
AI-generated content may contain errors. Please verify critical information