√28 - √63 + √175
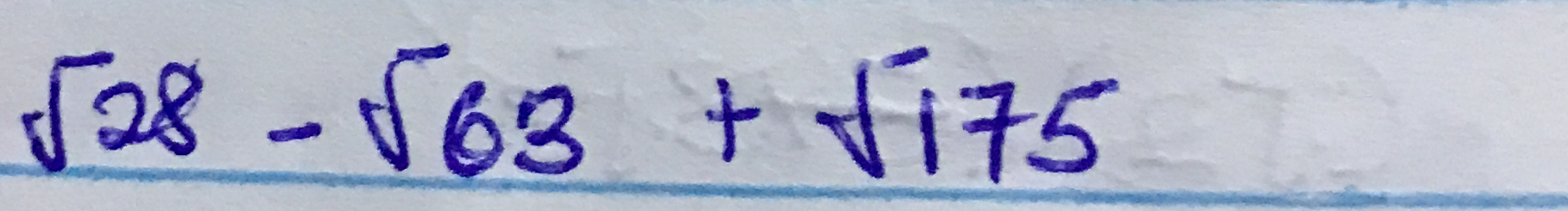
Understand the Problem
The question is asking for the simplification of the expression involving square roots: √28 - √63 + √175. We will simplify each square root individually and then combine the results.
Answer
The simplified expression is $4\sqrt{7}$.
Answer for screen readers
The simplified expression is $4\sqrt{7}$.
Steps to Solve
-
Simplify √28 To simplify $\sqrt{28}$, we can factor it as follows: $$\sqrt{28} = \sqrt{4 \cdot 7} = \sqrt{4} \cdot \sqrt{7} = 2\sqrt{7}$$
-
Simplify √63 Next, we simplify $\sqrt{63}$: $$\sqrt{63} = \sqrt{9 \cdot 7} = \sqrt{9} \cdot \sqrt{7} = 3\sqrt{7}$$
-
Simplify √175 Now, simplify $\sqrt{175}$: $$\sqrt{175} = \sqrt{25 \cdot 7} = \sqrt{25} \cdot \sqrt{7} = 5\sqrt{7}$$
-
Combine the results Now that we have simplified each square root, we can combine them: $$\sqrt{28} - \sqrt{63} + \sqrt{175} = 2\sqrt{7} - 3\sqrt{7} + 5\sqrt{7}$$
-
Combine like terms Combine the coefficients of $\sqrt{7}$: $$2\sqrt{7} - 3\sqrt{7} + 5\sqrt{7} = (2 - 3 + 5)\sqrt{7} = 4\sqrt{7}$$
The simplified expression is $4\sqrt{7}$.
More Information
Simplifying square roots involves factoring the numbers under the radicals into perfect squares. Here, we've recognized that 28, 63, and 175 can all be broken down using prime factorization, leading to the final simplified term.
Tips
- Forgetting to include a negative sign when simplifying or combining terms.
- Not recognizing perfect squares when simplifying square roots.
AI-generated content may contain errors. Please verify critical information