(√2)³ (√5)²
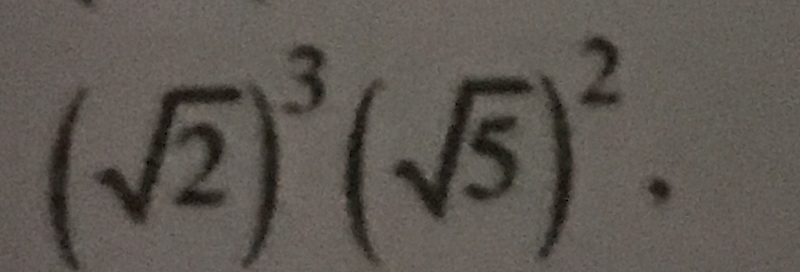
Understand the Problem
The question involves simplifying the expression which includes powers of square roots. We need to apply the properties of exponents and square roots to find the final simplified form.
Answer
The simplified expression is \( 10 \sqrt{2} \).
Answer for screen readers
The final simplified expression is ( 10 \sqrt{2} ).
Steps to Solve
- Rewrite the square root as an exponent
We can express the square roots as fractional exponents. Therefore, we have:
$$(\sqrt{2})^3 = (2^{1/2})^3$$
and
$$(\sqrt{5})^2 = (5^{1/2})^2.$$
- Apply the power of a power property
Using the property of exponents that states $(a^m)^n = a^{mn}$, we can simplify the expressions:
$$(2^{1/2})^3 = 2^{(1/2) \cdot 3} = 2^{3/2}$$
and
$$(5^{1/2})^2 = 5^{(1/2) \cdot 2} = 5^{1} = 5.$$
- Combine the results
Now we multiply the results together:
$$2^{3/2} \cdot 5.$$
- Rewrite using square roots
The expression $2^{3/2}$ can be rewritten as:
$$2^{3/2} = 2^{2/2} \cdot 2^{1/2} = 2 \cdot \sqrt{2}.$$
- Final expression
Combining everything, we have:
$$2 \sqrt{2} \cdot 5 = 10 \sqrt{2}.$$
The final simplified expression is ( 10 \sqrt{2} ).
More Information
This expression ( 10 \sqrt{2} ) represents a simplified form of the product of powers of square roots. This technique is helpful in various fields, particularly when dealing with equations involving radicals.
Tips
- Neglecting to multiply the bases correctly: Ensure each base is properly multiplied when combining terms.
- Confusing exponent rules: Remember that $(a^m)^n$ equals $a^{mn}$, and apply this consistently.
AI-generated content may contain errors. Please verify critical information