[2001][0 2 1]^T[5 1 6] = ( )
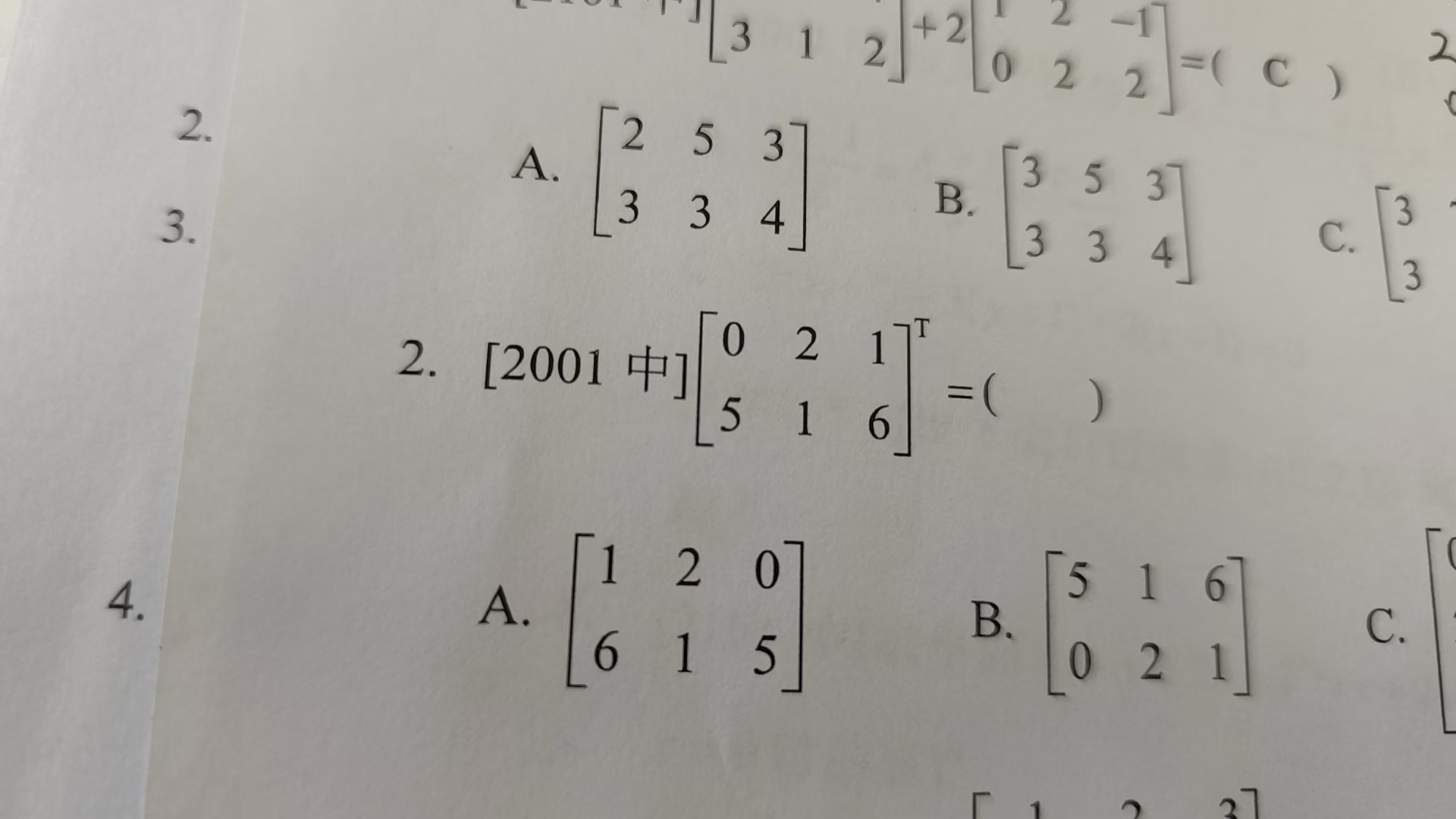
Understand the Problem
The question is asking to perform a matrix multiplication with a given matrix and a column vector and to find the resulting matrix. It involves calculating the product of the specified matrices and selecting the correct option from the provided choices.
Answer
The resulting matrix is \( \begin{bmatrix} 5 \\ 4007 \\ 2007 \end{bmatrix} \).
Answer for screen readers
The resulting matrix from the multiplication is:
$$ \begin{bmatrix} 5 \ 4007 \ 2007 \end{bmatrix} $$
Steps to Solve
- Identify the matrices and dimensions
We have the matrix ( A = \begin{bmatrix} 2001 & 0 \ 5 & 1 \ 6 \end{bmatrix} ) and the column vector ( B = \begin{bmatrix} 0 \ 2 \ 1 \end{bmatrix} ). The multiplication is between a matrix (3x3) and a column vector (3x1).
- Perform the matrix multiplication
To find the result ( C = A \cdot B ), we calculate each element of the resulting matrix using the formula:
$$ C[i, j] = A[i, :] \cdot B[:] $$
Calculating each entry:
-
First element (
C[1, 1]): $$ 2001 \cdot 0 + 0 \cdot 2 + 5 \cdot 1 = 0 + 0 + 5 = 5 $$ -
Second element (
C[2, 1]): $$ 2001 \cdot 2 + 0 \cdot 0 + 5 \cdot 1 = 4002 + 0 + 5 = 4007 $$ -
Third element (
C[3, 1]): $$ 2001 \cdot 1 + 0 \cdot 2 + 6 \cdot 1 = 2001 + 0 + 6 = 2007 $$
- Construct the resulting matrix
Now, assemble the computed values into a matrix format. The resulting matrix is:
$$ C = \begin{bmatrix} 5 \ 4007 \ 2007 \end{bmatrix} $$
It is important to note that the multiplication was performed element-wise as described.
The resulting matrix from the multiplication is:
$$ \begin{bmatrix} 5 \ 4007 \ 2007 \end{bmatrix} $$
More Information
The answer shows the result of multiplying a matrix with a vector. Matrix multiplication is a linear transformation, where each element is computed as a dot product of corresponding rows and columns.
Tips
- Miscalculating products or sums during matrix multiplication. Always ensure that you multiply corresponding entries correctly.
- Forgetting to consider the dimensions of the matrices involved; ensure they are compatible for multiplication.
AI-generated content may contain errors. Please verify critical information