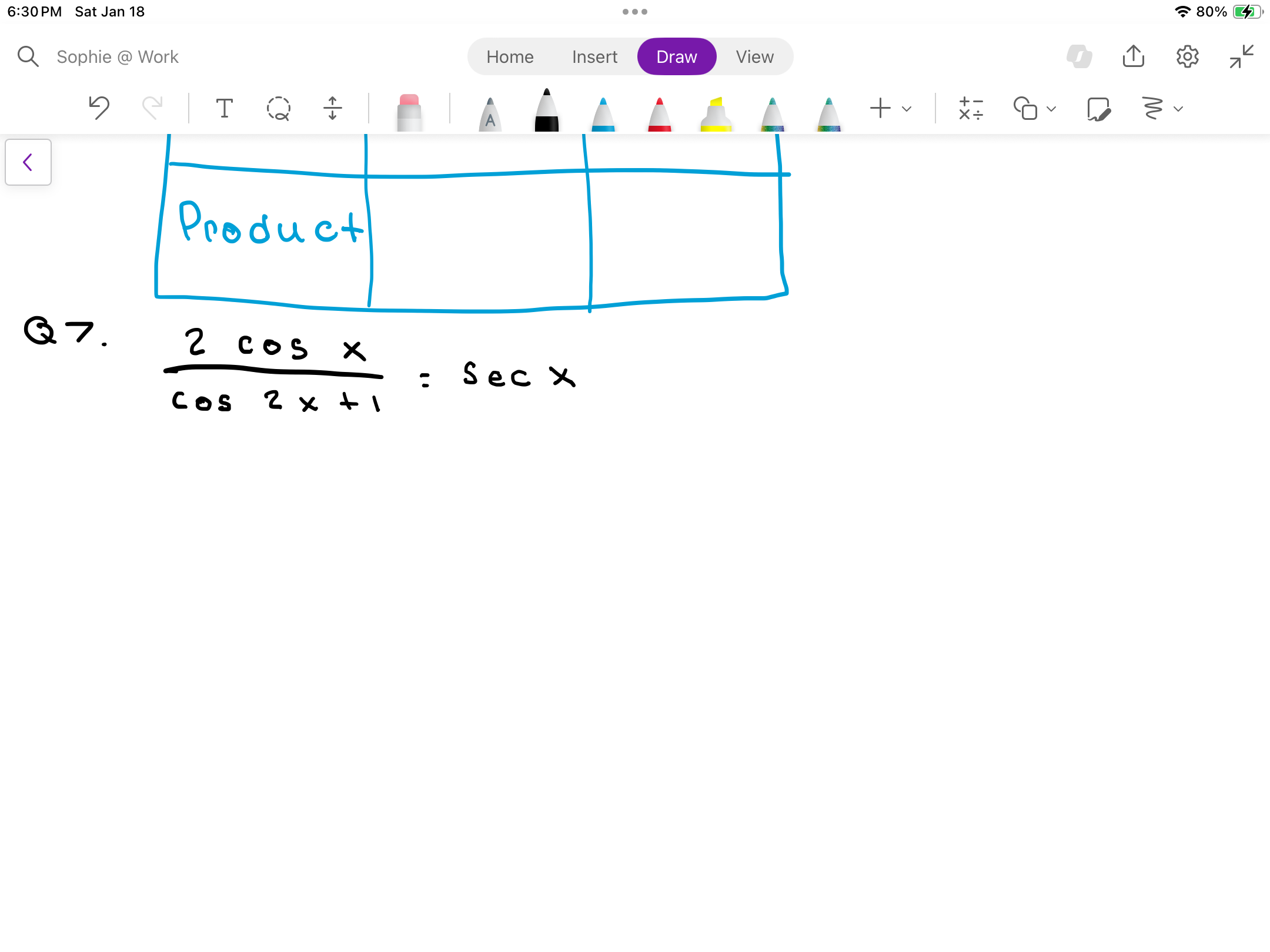
2 cos x / (cos 2x + 1) = sec x
Understand the Problem
The question involves solving a trigonometric equation involving cosine and secant functions. It asks for a simplification or verification that the left side equals the right side.
Answer
The equation is verified; it holds true for \( x \) where \( \cos x \neq 0 \).
Answer for screen readers
The equation is verified; it holds true for ( x ) where ( \cos x \neq 0 ).
Steps to Solve
-
Identify the equation
We start with the equation:
$$ \frac{2 \cos x}{\cos 2x + 1} = \sec x $$ -
Express secant in terms of cosine
Recall that secant is the reciprocal of cosine: $$ \sec x = \frac{1}{\cos x} $$
Thus, we rewrite the right side: $$ \frac{2 \cos x}{\cos 2x + 1} = \frac{1}{\cos x} $$ -
Cross-multiply to eliminate the fraction
Cross-multiplying gives us: $$ 2 \cos^2 x = \cos 2x + 1 $$ -
Use the double angle identity for cosine
Recall the double angle identity: $$ \cos 2x = 2 \cos^2 x - 1 $$
Substituting this into the equation gives: $$ 2 \cos^2 x = (2 \cos^2 x - 1) + 1 $$ -
Simplify the equation
The equation simplifies to: $$ 2 \cos^2 x = 2 \cos^2 x $$
This is an identity, meaning it holds for all ( x ) where ( \cos x \neq 0 ).
The equation is verified; it holds true for ( x ) where ( \cos x \neq 0 ).
More Information
This trigonometric identity shows that the left side equals the right side under the condition that ( \cos x ) is not zero. Thus, the original equation is valid for many values of ( x ).
Tips
- Forgetting to use trigonometric identities such as the double angle identities can lead to incorrect simplifications.
- Misapplying the reciprocal property of secant (i.e., not realizing that ( \sec x = \frac{1}{\cos x} )).
AI-generated content may contain errors. Please verify critical information