-2 * [[-2, 4], [-3, -6]] is equal to which matrix?
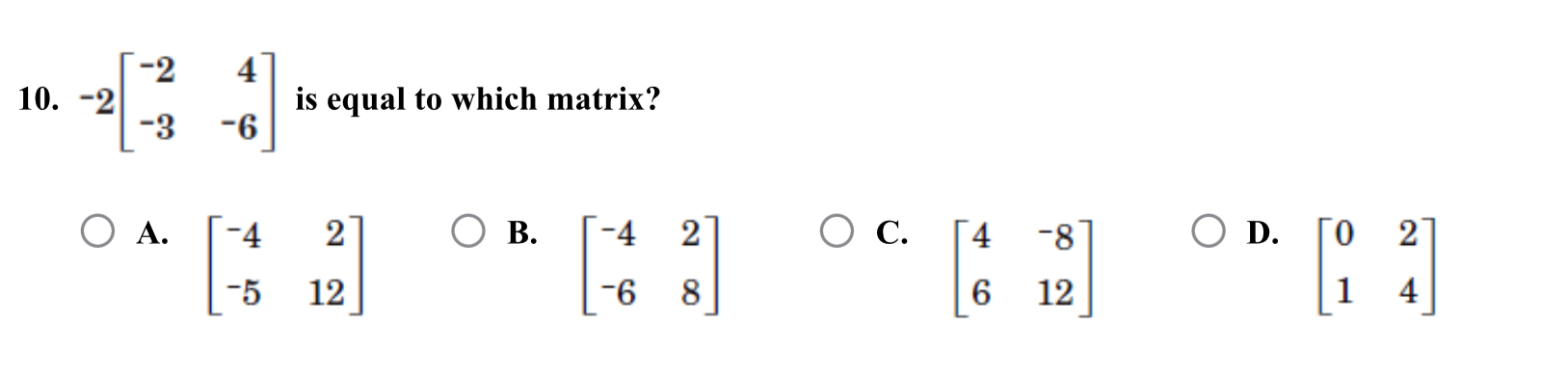
Understand the Problem
The question is asking to determine which matrix equals the result of multiplying the given matrix by -2.
Answer
The resultant matrix is $$ \begin{bmatrix} 4 & -8 \\ 6 & 12 \end{bmatrix} $$
Answer for screen readers
The matrix obtained after multiplication is
$$ \begin{bmatrix} 4 & -8 \ 6 & 12 \end{bmatrix} $$
Steps to Solve
- Multiply each element by -2
To find the resulting matrix, multiply each element in the given matrix by -2:
[ -2 \cdot \begin{bmatrix} -2 & 4 \ -3 & -6 \end{bmatrix} = \begin{bmatrix} -2 \cdot -2 & -2 \cdot 4 \ -2 \cdot -3 & -2 \cdot -6 \end{bmatrix} ]
- Calculate each element step-by-step
Perform the multiplication for each element:
-
Top left: $-2 \cdot -2 = 4$
-
Top right: $-2 \cdot 4 = -8$
-
Bottom left: $-2 \cdot -3 = 6$
-
Bottom right: $-2 \cdot -6 = 12$
- Construct the resultant matrix
Combine the calculated values to form the resultant matrix:
[ \begin{bmatrix} 4 & -8 \ 6 & 12 \end{bmatrix} ]
The matrix obtained after multiplication is
$$ \begin{bmatrix} 4 & -8 \ 6 & 12 \end{bmatrix} $$
More Information
This result indicates that multiplying each element of the original matrix by a negative constant transforms the values to their negatives and scales them accordingly.
Tips
- Forgetting to multiply both rows or mixing up the signs in the multiplication can lead to incorrect matrices.
- Not applying the multiplication to every element of the matrix.
AI-generated content may contain errors. Please verify critical information