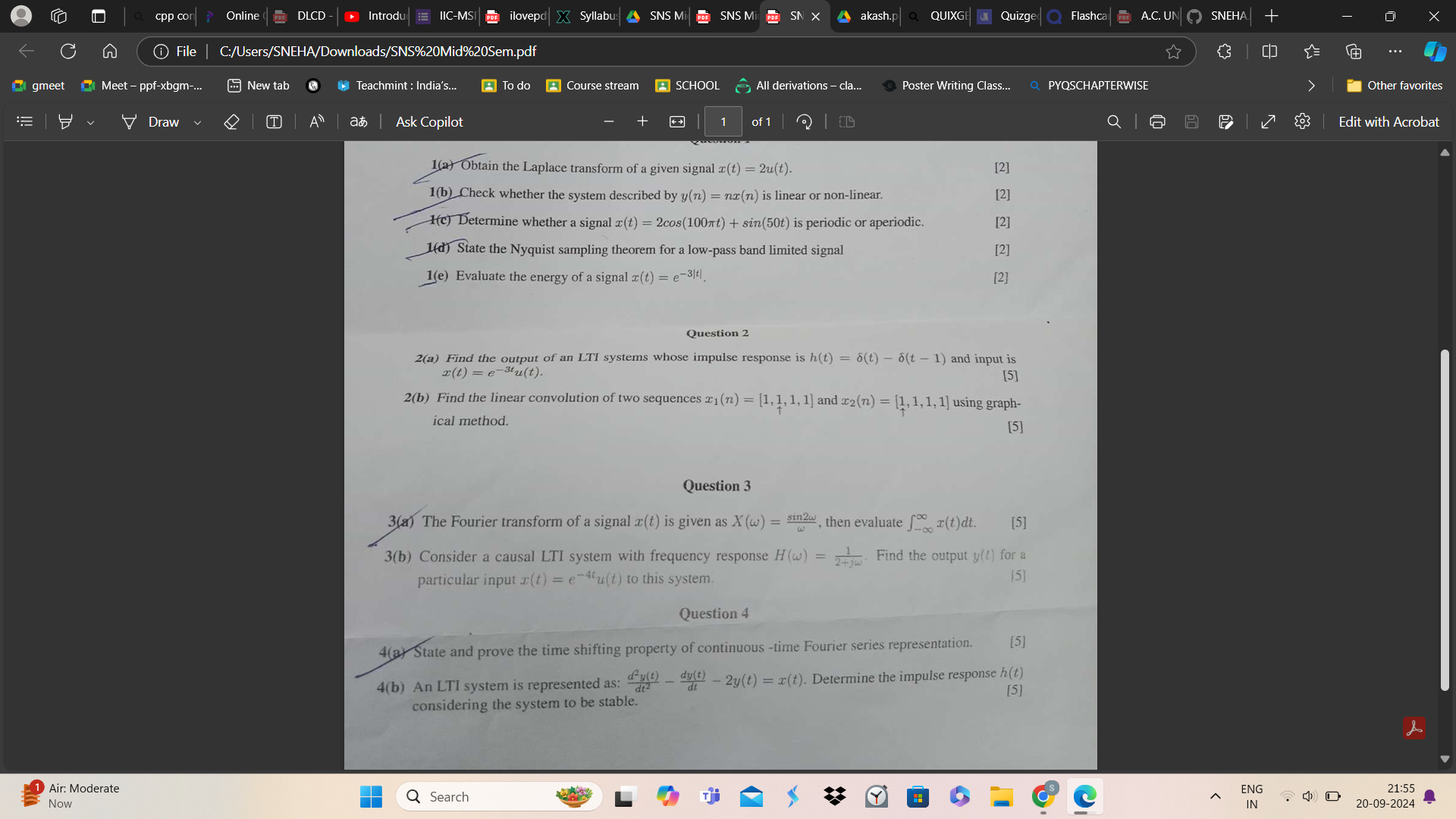
1(a) Obtain the Laplace transform of a given signal x(t) = 2u(t). 1(b) Check whether the system described by y(n) = nx(n) is linear or non-linear. 1(c) Determine whether a signal x... 1(a) Obtain the Laplace transform of a given signal x(t) = 2u(t). 1(b) Check whether the system described by y(n) = nx(n) is linear or non-linear. 1(c) Determine whether a signal x(t) = 2cos(100πt) + sin(50t) is periodic or aperiodic. 1(d) State the Nyquist sampling theorem for a low-pass band limited signal. 1(e) Evaluate the energy of a signal x(t) = e^(-3t). 2(a) Find the output of an LTI system whose impulse response is h(t) = δ(t) - δ(t - 1) and input is x(t) = e^(-3t)u(t). 2(b) Find the linear convolution of two sequences z1(n) = [1, 1, 1, 1] and z2(n) = [1, 1, 1, 1] using graphical method. 3(a) The Fourier transform of a signal x(t) is given as X(ω) = sin(2ω)/ω, then evaluate ∫_{-∞}^{∞} x(t) dt. 3(b) Consider a causal LTI system with frequency response H(ω) = 1/(2+jω). Find the output y(t) for a particular input x(t) = e^(-4t)u(t) to this system. 4(a) State and prove the time shifting property of continuous-time Fourier series representation. 4(b) An LTI system is represented as: d^3y(t)/dt^3 - dy(t)/dt - 2y(t) = x(t). Determine the impulse response h(t) considering the system to be stable. Read more

Steps to Solve

1. Obtain the Laplace Transform of $x(t)$

For the signal $x(t) = 2u(t)$, we will use the Laplace transform formula:

$$ X(s) = \int_0^{\infty} x(t) e^{-st} dt $$

Substituting the function:

$$ X(s) = \int_0^{\infty} 2 e^{-st} dt $$

2. Evaluate the integral

The integral can be solved as follows:

$$ X(s) = 2 \int_0^{\infty} e^{-st} dt = 2 \left[-\frac{1}{s} e^{-st} \right]_0^{\infty} $$

Evaluating the limits gives:

$$ X(s) = 2 \left[0 + \frac{1}{s}\right] = \frac{2}{s} \text{ for } Re(s) > 0 $$

3. Check if the system is linear or non-linear

To check if the system given by $y(n) = nx(n)$ is linear, test for the superposition principle:

Let $x_1(n)$ and $x_2(n)$ be two input sequences. We check:

$$ y_1(n) + y_2(n) = n x_1(n) + n x_2(n) = n(x_1(n) + x_2(n)) $$

Since it holds true for any input, the system is linear.

4. Determine periodicity.

For $x(t) = 2\cos(100\pi t) + \sin(50t)$:

The term $2\cos(100\pi t)$ has a period of $T_1 = \frac{2\pi}{100\pi} = \frac{1}{50}$,

The term $\sin(50t)$ has a period of $T_2 = \frac{2\pi}{50} = \frac{\pi}{25}$.

To find the least common multiple (LCM):

$$ \text{lcm}(T_1, T_2) = \text{lcm}\left(\frac{1}{50}, \frac{\pi}{25}\right) = \frac{1}{50} $$

Thus, the overall signal $x(t)$ is periodic.

5. Apply the Nyquist Sampling Theorem

The Nyquist theorem states that the sampling frequency must be at least twice the maximum frequency:

$$ f_s \geq 2 \cdot 50 = 100 \text{ Hz} $$

6. Evaluate the energy of the signal $x(t) = e^{-3t}u(t)$

The energy $E$ is given by:

$$ E = \int_{-\infty}^{\infty} |x(t)|^2 dt = \int_0^{\infty} (e^{-3t})^2 dt = \int_0^{\infty} e^{-6t} dt $$

Solving this gives:

$$ E = \left[-\frac{1}{6} e^{-6t}\right]_0^{\infty} = \frac{1}{6} $$