18. a. Evaluate √100. b. Evaluate √36 + √64. c. Is it true that √100 = √36 + √64?
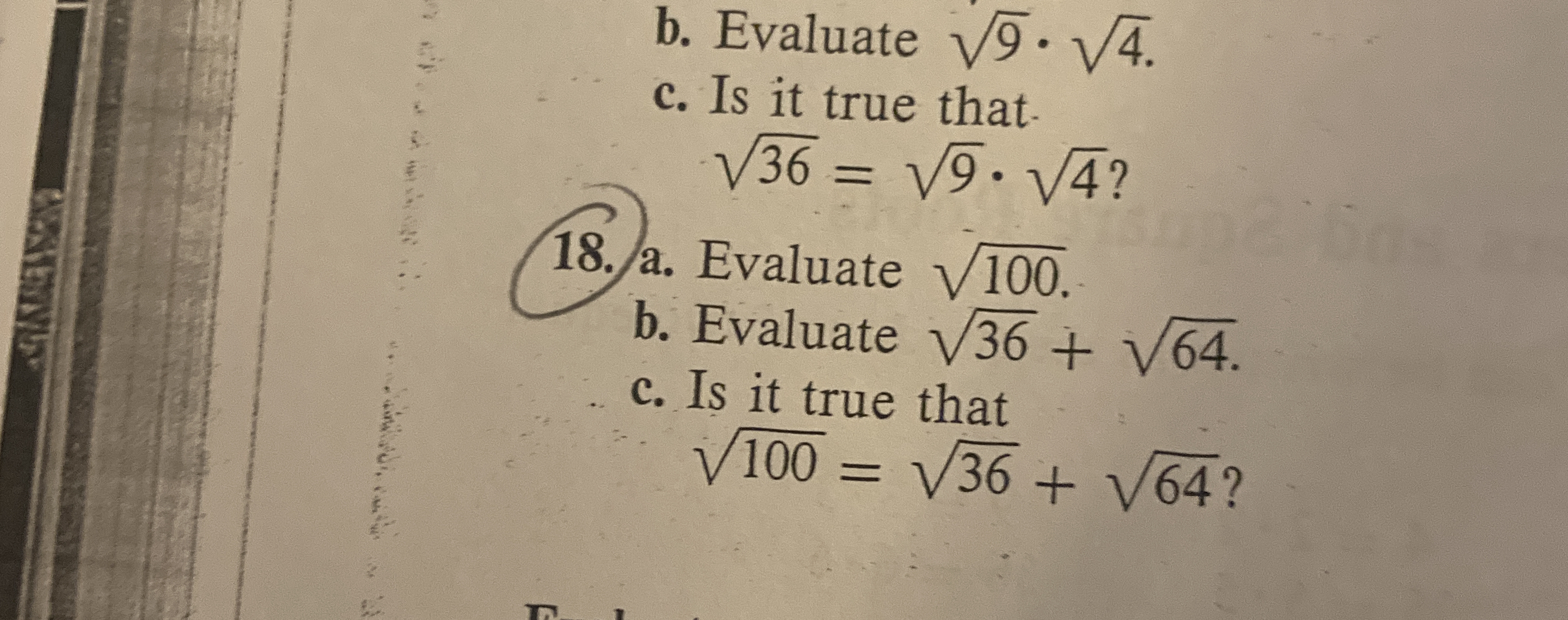
Understand the Problem
The question requires evaluating square roots of numbers and checking if a mathematical equality holds. Specifically, it asks to evaluate the square root of 100, sum the square roots of 36 and 64, and determine if the square root of 100 equals that sum.
Answer
No, \( \sqrt{100} \neq \sqrt{36} + \sqrt{64} \).
Answer for screen readers
No, it is not true that ( \sqrt{100} = \sqrt{36} + \sqrt{64} ).
Steps to Solve
- Evaluate √100
The square root of 100 can be calculated:
$$ \sqrt{100} = 10 $$
- Evaluate √36 + √64
First, evaluate each square root:
- The square root of 36 is:
$$ \sqrt{36} = 6 $$
- The square root of 64 is:
$$ \sqrt{64} = 8 $$
Now, sum them up:
$$ \sqrt{36} + \sqrt{64} = 6 + 8 = 14 $$
- Check the equality
Now, we need to check if:
$$ \sqrt{100} = \sqrt{36} + \sqrt{64} $$
Substituting the values we calculated:
$$ 10 = 14 $$
This equality is not true.
No, it is not true that ( \sqrt{100} = \sqrt{36} + \sqrt{64} ).
More Information
The square root function gives the principal non-negative root of a number. Additionally, it’s useful to know that ( \sqrt{a} + \sqrt{b} ) does not necessarily equal ( \sqrt{a + b} ).
Tips
- Confusing the addition of square roots with the square root of sums. Remember that ( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} ).
- Forgetting to simplify expressions properly.
AI-generated content may contain errors. Please verify critical information