√16x * √16x^5
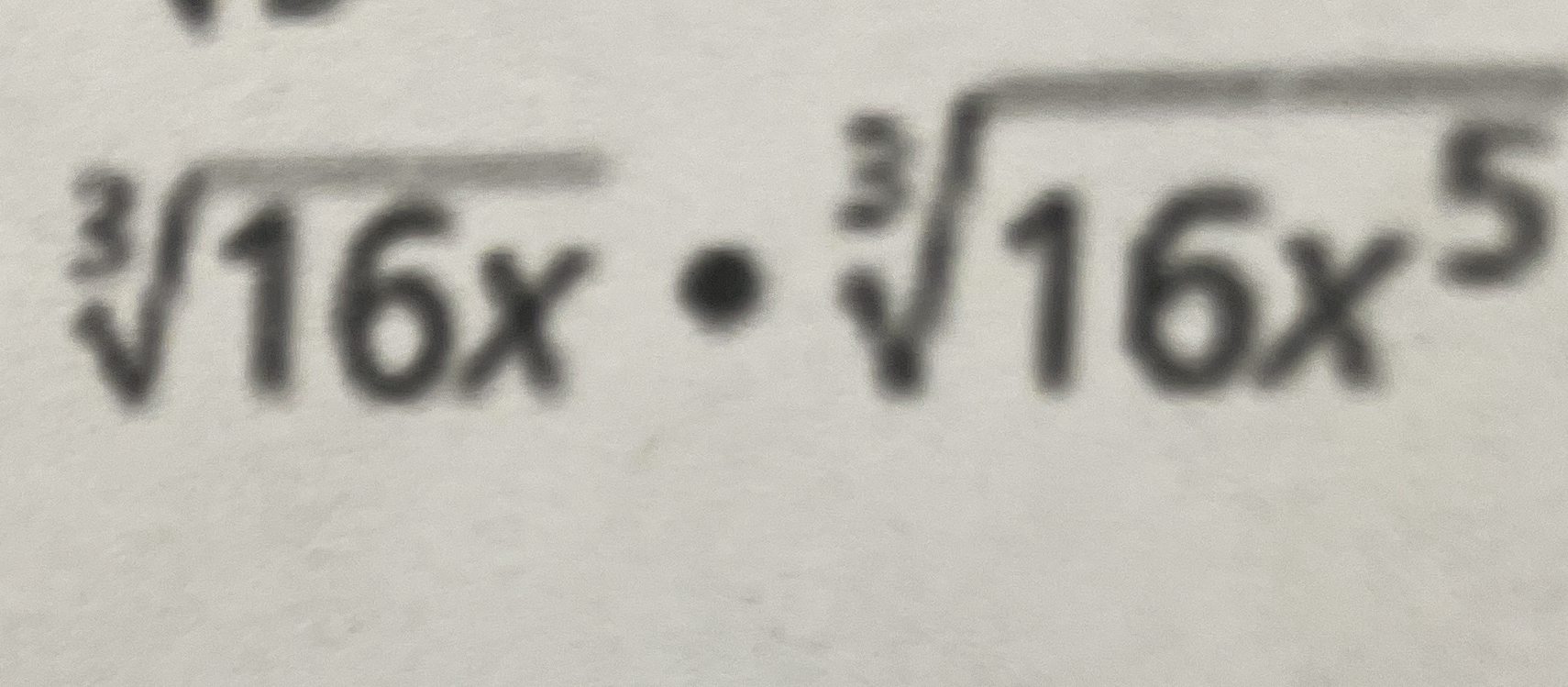
Understand the Problem
The question is asking us to simplify or evaluate the expression involving square roots and variables. Specifically, it involves multiplying two radical expressions: the cube root of 16x and the square root of 16x raised to the 5th power.
Answer
The simplified expression is \( 4096x^3 \).
Answer for screen readers
The simplified expression is ( 4096x^3 ).
Steps to Solve
- Express the square roots as exponents
The square root can be represented with exponents: $$ \sqrt{16x} = (16x)^{1/2} $$
After this, we have: $$ \sqrt{16x} \cdot \sqrt{16x^5} = (16x)^{1/2} \cdot (16x^5)^{1/2} $$
- Simplify each expression
Now we can apply the exponent rule $(a^m \cdot a^n = a^{m+n})$ to combine the two terms: $$ (16x)^{1/2} \cdot (16x^5)^{1/2} = (16x)^{1/2 + 1/2} = (16x)^{(1 + 5)/2} $$
- Combine the exponents
Simplifying gives: $$ (16x)^{(1 + 5)/2} = (16x)^{6/2} = (16x)^{3} $$
- Expanding the expression
Next, we will expand ( (16x)^3 ): $$ (16x)^3 = 16^3 \cdot x^3 $$
Calculating ( 16^3 ): $$ 16^3 = 4096 $$
Thus: $$ (16x)^3 = 4096x^3 $$
The simplified expression is ( 4096x^3 ).
More Information
This expression illustrates how to use the properties of exponents and radical expressions effectively. The cube of 16 represents a large number, and this example shows how combining square roots can lead to polynomial expressions in algebra.
Tips
- Mistaking the rules of exponents: Ensure that when multiplying terms with the same base, you add the exponents correctly.
- Forgetting to convert roots to exponents before simplifying.
AI-generated content may contain errors. Please verify critical information