12x^5y - 3xy^{10} + 21x^{15}y^4 ÷ 3x^5y is equivalent to which of the options?

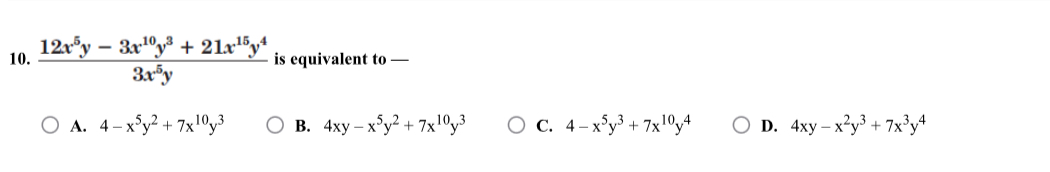
Understand the Problem

The question is asking to simplify the given expression and determine which of the four provided options is equivalent to it. We need to perform algebraic simplification involving division of polynomials.

Answer

$$ 4 - x^{-4}y^{9} + 7x^{10}y^{3} $$

Steps to Solve

Divide Each Term by the Denominator
We start by dividing each term in the numerator by the denominator $3x^5y$.

The terms are:

$12x^5y ÷ 3x^5y = \frac{12}{3} = 4$
$-3xy^{10} ÷ 3x^5y = -\frac{3}{3} \cdot \frac{y^{10}}{y} \cdot \frac{x}{x^5} = -1 \cdot y^{9} \cdot x^{-4} = -\frac{y^{9}}{x^{4}}$
$21x^{15}y^{4} ÷ 3x^5y = \frac{21}{3} \cdot x^{15-5} \cdot y^{4-1} = 7x^{10}y^{3}$

Now the expression simplifies to:
$$ 4 - \frac{y^{9}}{x^{4}} + 7x^{10}y^{3} $$

Rewrite the Expression
Rewriting the expression gives:
$$ 4 + 7x^{10}y^{3} - \frac{y^{9}}{x^{4}} $$
Combine Terms
Now, we need to ensure it's in a standard form. The term $-\frac{y^{9}}{x^{4}}$ can be rewritten with a common denominator if needed.
Final Expression
Combine all terms appropriately to match given options.

$$ 4 - x^{-4}y^{9} + 7x^{10}y^{3} $$

More Information

The process of simplifying involves breaking down term by term by dividing each by the common denominator. This is especially useful in handling polynomials and ensures all components are accounted for correctly.

Tips

Failing to distribute the division across all terms correctly.
Forgetting to reduce the powers of $x$ and $y$ when dividing.
Misplacing terms or the sign when rewriting the expression.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!