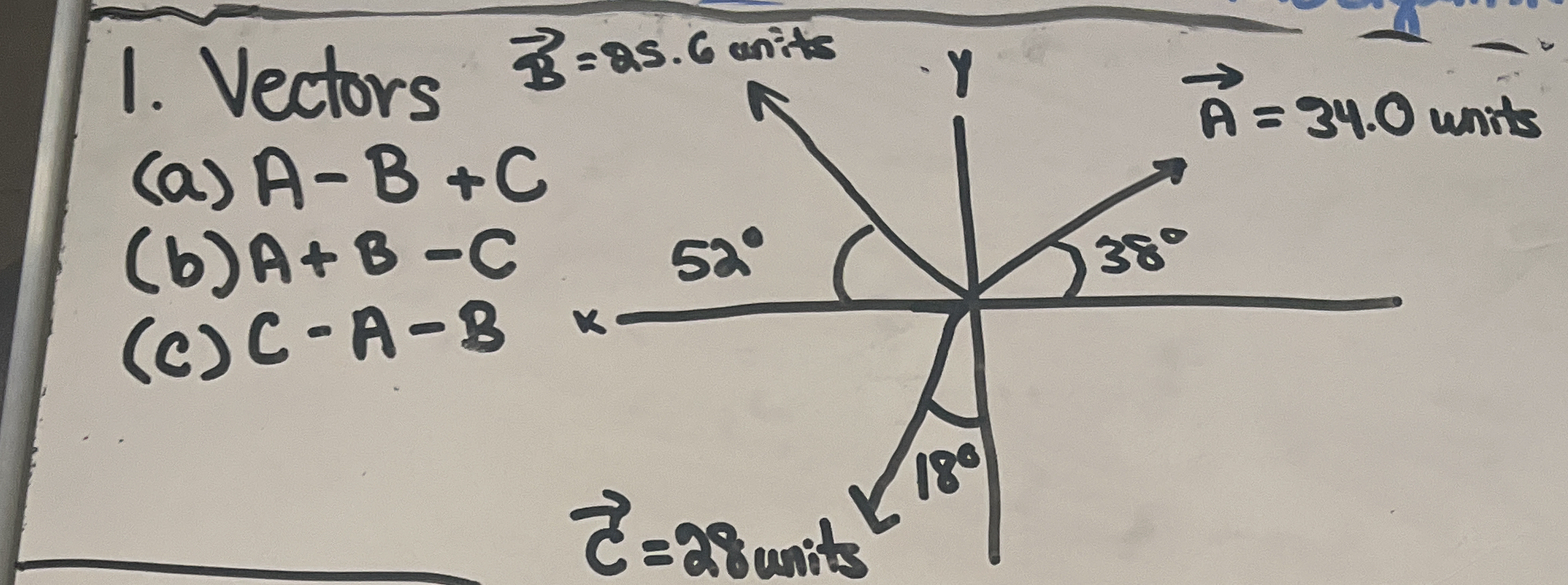
1. Vectors (a) A - B + C (b) A + B - C (c) C - A - B

Steps to Solve

1. Identify the Vectors' Components

   Given the vectors, we need to resolve each vector into its x and y components using the provided angles:

   For vector $A$:

   • Magnitude = 34.0 units, angle = 38°
   • Components:
     • $A_x = A \cdot \cos(38^\circ)$
     • $A_y = A \cdot \sin(38^\circ)$

   For vector $C$:

   • Magnitude = 28.0 units, angle = 180° - 18° = 162°
   • Components:
     • $C_x = C \cdot \cos(162^\circ)$
     • $C_y = C \cdot \sin(162^\circ)$

   For vector $B$:

   • Magnitude = 95.6 units, angle = 52°
   • Components:
     • $B_x = B \cdot \cos(52^\circ)$
     • $B_y = B \cdot \sin(52^\circ)$

2. Calculate Each Vector's Components

   Calculate the components using the cosine and sine functions:

   [ A_x = 34.0 \cdot \cos(38^\circ), \quad A_y = 34.0 \cdot \sin(38^\circ) ]

   [ C_x = 28.0 \cdot \cos(162^\circ), \quad C_y = 28.0 \cdot \sin(162^\circ) ]

   [ B_x = 95.6 \cdot \cos(52^\circ), \quad B_y = 95.6 \cdot \sin(52^\circ) ]

3. Solve for Each Vector's Components

   Now calculate the values:

   By using a calculator for each component:

   • $A_x \approx 34.0 \cdot 0.7880 \approx 26.8$ units
   • $A_y \approx 34.0 \cdot 0.6157 \approx 20.9$ units
   • $C_x \approx 28.0 \cdot (-0.9511) \approx -26.6$ units
   • $C_y \approx 28.0 \cdot 0.3090 \approx 8.6$ units
   • $B_x \approx 95.6 \cdot 0.6157 \approx 58.8$ units
   • $B_y \approx 95.6 \cdot 0.7880 \approx 75.4$ units

4. Perform Vector Operations

   For (a): $A - B + C$

   The components will be:

   • $X$ component: $A_x - B_x + C_x$
   • $Y$ component: $A_y - B_y + C_y$

   For (b): $A + B - C$

   The components will be:

   • $X$ component: $A_x + B_x - C_x$
   • $Y$ component: $A_y + B_y - C_y$

   For (c): $C - A - B$

   The components will be:

   • $X$ component: $C_x - A_x - B_x$
   • $Y$ component: $C_y - A_y - B_y$

5. Find the Resultant Vectors

   After performing each operation: Resultant vector magnitude can be calculated as:

   $$ R = \sqrt{R_x^2 + R_y^2} $$

   And the angle as:

   $$ \theta = \tan^{-1}\left(\frac{R_y}{R_x}\right) $$