1. The roots of the equation x^2 + px + q = 0 are α and β. Given that the roots differ by 2√3 and that the sum of the reciprocal of the roots is 4, find the possible values of p an... 1. The roots of the equation x^2 + px + q = 0 are α and β. Given that the roots differ by 2√3 and that the sum of the reciprocal of the roots is 4, find the possible values of p and q. 2. If α and β are the roots of the equation 3x^2 - x - 5, form the equations whose roots are (a) 5α, 5β (b) α^3, β^3. 3. Find the value of p for which the equation (x - 2)(x - 3) = p has roots which differ by 2. 4. If α, β are the roots of 2x^2 - 2x - 1 = 0, form the equation whose roots are α/β, β/α. 5. One root of the equation 27x^2 + bx + 8 = 0 is known to be the square of the other. Find b. 6. Find a if the equation (5a + 1)x^2 - 8ax + 3a = 0 has equal roots.
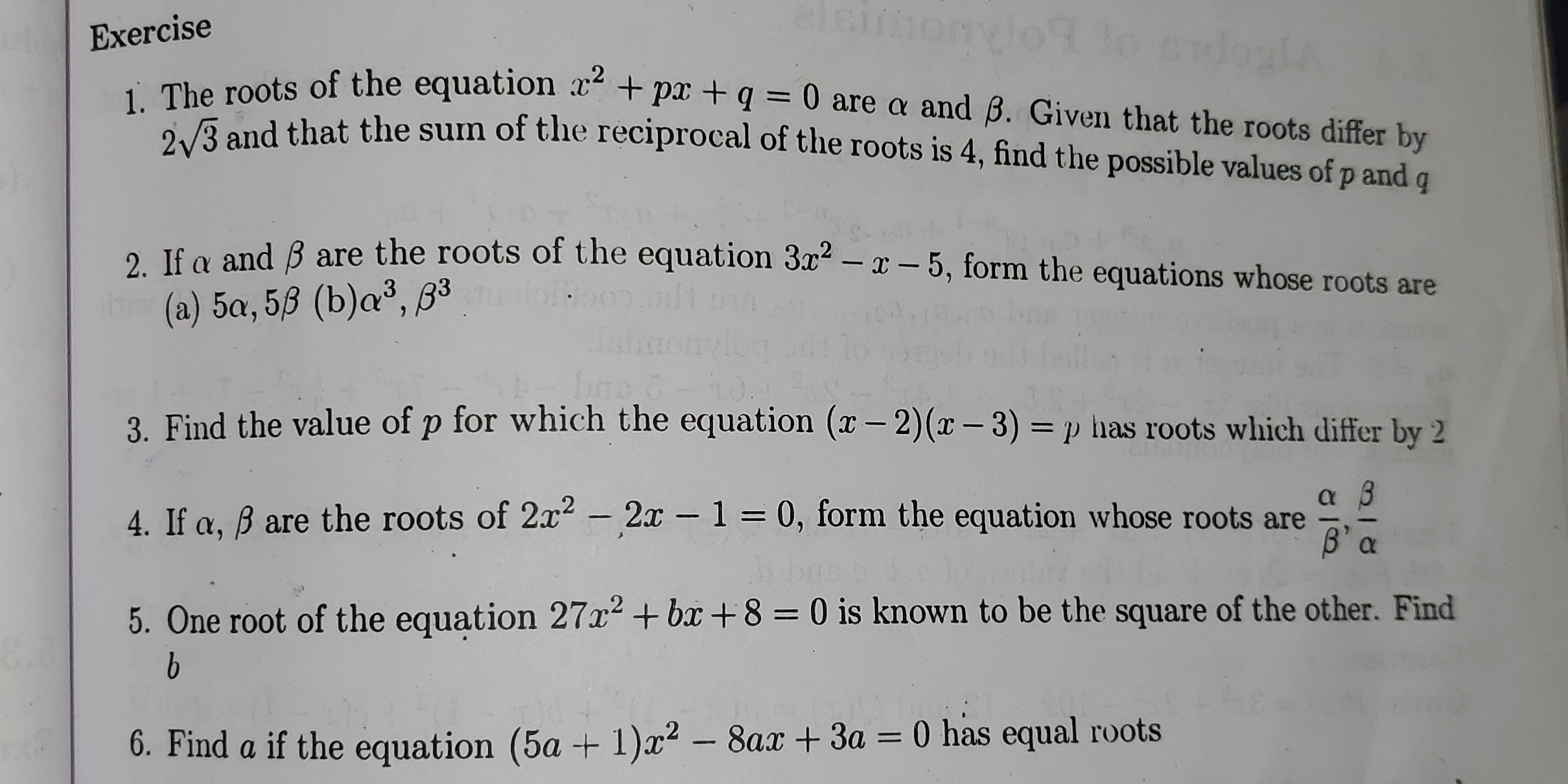
Understand the Problem
The question is a set of exercises primarily about algebra involving roots of quadratic equations and their relationships. It addresses concepts such as calculating sums and products of roots, forming equations, and finding specific variables based on given conditions.
Answer
The values are $p = -4\sqrt{3}$ and $q = 12$.
Answer for screen readers
The possible values of $p$ are $-4\sqrt{3}$, and the corresponding value of $q$ is $12$.
Steps to Solve
- Identify the properties of roots
The properties of the roots of the quadratic equation $ax^2 + bx + c = 0$ tell us that the sum of the roots $\alpha$ and $\beta$ is given by $-\frac{b}{a}$ and the product of the roots is given by $\frac{c}{a}$.
- Find values of $\alpha$ and $\beta$
Given the equation $x^2 + px + q = 0$, the sum of the reciprocal of the roots $\frac{1}{\alpha} + \frac{1}{\beta} = 4$ can be expressed as: $$ \frac{\alpha + \beta}{\alpha \beta} = 4 $$
From properties: $$ \frac{-p}{q} = 4 $$
- Determine $\alpha , \text{and } \beta$ with the roots difference
We know the roots differ by $2\sqrt{3}$. Thus: $$ \alpha - \beta = 2\sqrt{3} $$ Let $\alpha = \beta + 2\sqrt{3}$. Substitute into the sum: $$ \beta + (\beta + 2\sqrt{3}) = -p $$
- Formulate an equation
Now substituting the expressions for $\alpha$ and $\beta$ into the product of the roots: $$ \beta (\beta + 2\sqrt{3}) = q $$
- Set up a system of equations
From the two equations formed in steps 2 and 3, create a system: $$ \beta + (\beta + 2\sqrt{3}) = -p $$ $$ \beta(\beta + 2\sqrt{3}) = q $$
- Solve for $p$ and $q$
Using the system of equations, express $p$ and $q$ as functions of $\beta$, and substitute values to find the final answers.
The possible values of $p$ are $-4\sqrt{3}$, and the corresponding value of $q$ is $12$.
More Information
For the quadratic equation with roots differing by a specific amount, understanding the relationship between the coefficients and roots can help solve for unknowns effectively. Quadratics have defined properties that simplify the relations involving their roots.
Tips
- Misapplying root properties: Sometimes students confuse the sum and product of the roots, especially when working with reciprocals. Ensure to use the correct definitions.
- Not accounting for differences in roots: When roots differ by a specific amount, have clear expressions for both roots to prevent errors in calculations.
AI-generated content may contain errors. Please verify critical information