1. Solve d²y/dx² - 4dy/dx + 3y = 0. 2. Solve the differential equations d³y/dx³ - d²y/dx² - 12dy/dx = 0. 3. Solve (i) d³y/dx² - 13dy/dx + 12y = 0; (ii) d³y/dx³ - 9d²y/dx² + 25y = 0... 1. Solve d²y/dx² - 4dy/dx + 3y = 0. 2. Solve the differential equations d³y/dx³ - d²y/dx² - 12dy/dx = 0. 3. Solve (i) d³y/dx² - 13dy/dx + 12y = 0; (ii) d³y/dx³ - 9d²y/dx² + 25y = 0. 4. Solve d³y/dx³ - 3d²y/dx² + 4y = 0.
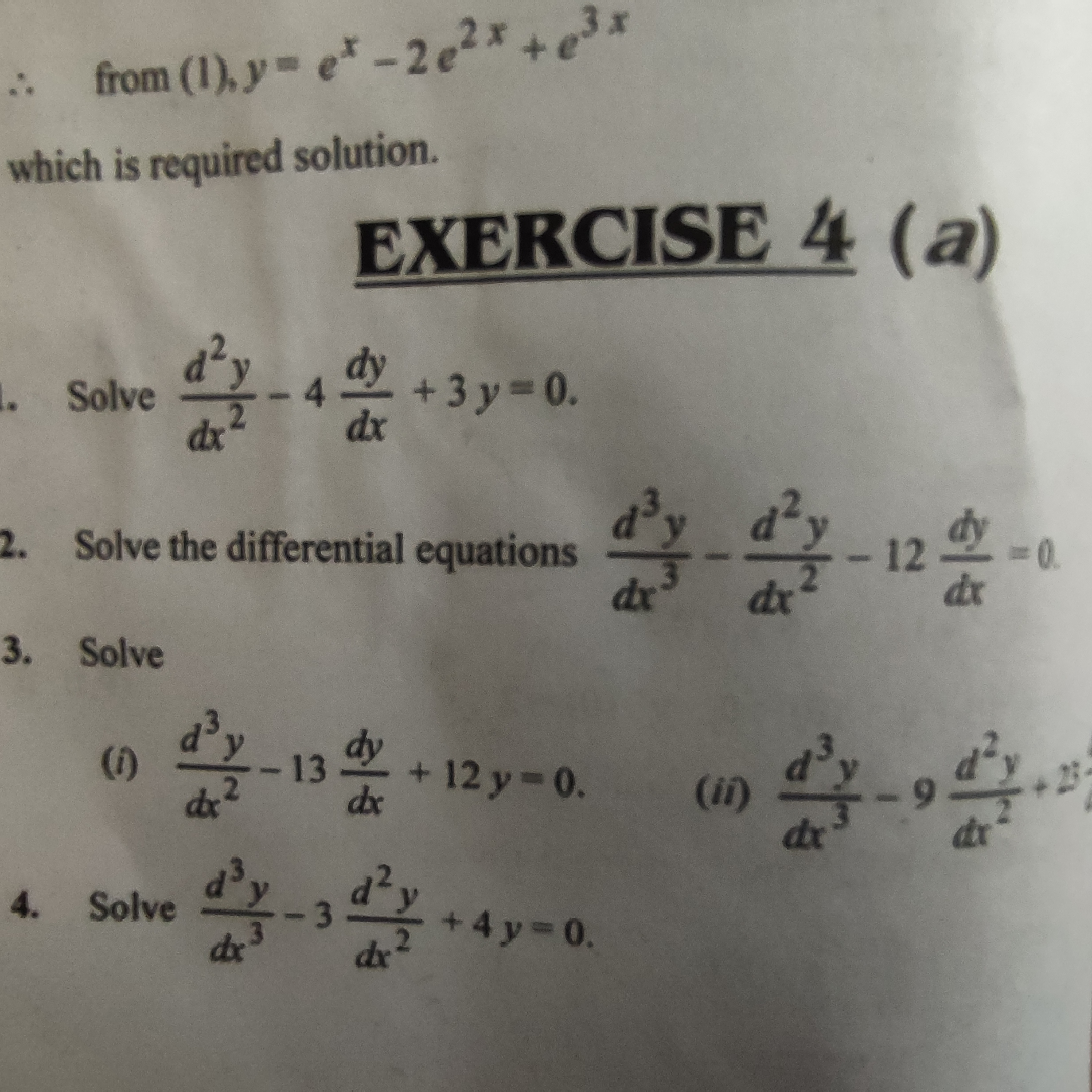
Understand the Problem
The question is asking to solve a series of differential equations, which involve operations such as taking derivatives. The user needs solutions for various forms of equations listed under exercise 4.
Answer
Answer for screen readers
-
$$ y = C_1 e^x + C_2 e^{3x} $$
-
$$ y = C_1 + C_2 e^{4x} + C_3 e^{-3x} $$
-
(i) $$ y = C_1 e^x + C_2 e^{3x} + C_3 e^{-4x} $$
Steps to Solve
- Solve the first equation
Let's start with the equation: $$ \frac{d^2y}{dx^2} - 4\frac{dy}{dx} + 3y = 0 $$
First, we find the characteristic equation: $$ r^2 - 4r + 3 = 0 $$
Next, factor the quadratic: $$(r - 1)(r - 3) = 0 $$
Thus, the roots are $r = 1$ and $r = 3$. The general solution is: $$ y = C_1 e^x + C_2 e^{3x} $$
- Solve the second equation
Now consider: $$ \frac{d^3y}{dx^3} - \frac{d^2y}{dx^2} - 12\frac{dy}{dx} = 0 $$
The characteristic equation is: $$ r^3 - r^2 - 12r = 0 $$
Factoring out an $r$ gives: $$ r(r^2 - r - 12) = 0 $$
Factoring the quadratic: $$(r - 4)(r + 3) = 0 $$
Thus, the roots are $r = 0$, $r = 4$, and $r = -3$. The general solution is: $$ y = C_1 + C_2 e^{4x} + C_3 e^{-3x} $$
- Solve the third equation (i)
Now, for the equation: $$ \frac{d^3y}{dx^3} - 13\frac{dy}{dx} + 12y = 0 $$
The characteristic equation is: $$ r^3 - 13r + 12 = 0 $$
Using synthetic division or trial and error, we find that $r = 1$ is a root. Factoring gives: $$ (r - 1)(r^2 + r - 12) = 0 $$
Factoring further: $$(r - 1)(r - 3)(r + 4) = 0 $$
Thus, the roots are $r = 1$, $r = 3$, and $r = -4$. The general solution is: $$ y = C_1 e^x + C_2 e^{3x} + C_3 e^{-4x} $$
- Solve the third equation (ii)
Now for: $$ \frac{d^3y}{dx^3} - 9\frac{d^2y}{dx^2} + 25y = 0 $$
The characteristic equation is: $$ r^3 - 9r^2 + 25 = 0 $$
Using the rational root theorem, guess $r = 5$ is a root. Thus, factor: $$ (r - 5)(r^2 - 4r + 5) = 0 $$
The quadratic gives: $$ r = 2 \pm i $$
Thus, the roots are $r = 5$, $r = 2 + i$, and $r = 2 - i$. The general solution is: $$ y = C_1 e^{5x} + e^{2x}(C_2 \cos x + C_3 \sin x) $$
- Solve the fourth equation
Finally, for: $$ \frac{d^3y}{dx^3} - 3\frac{d^2y}{dx^2} + 4y = 0 $$
The characteristic equation is: $$ r^3 - 3r^2 + 4 = 0 $$
Using trial, $r = 2$ is a root. Thus, factor: $$ (r - 2)(r^2 - r - 2) = 0 $$
This gives: $$(r - 2)(r - 2)(r + 1) = 0 $$
Thus, the roots are $r = 2$ (double root) and $r = -1$. The general solution is: $$ y = C_1 e^{2x} + C_2 xe^{2x} + C_3 e^{-x} $$
-
$$ y = C_1 e^x + C_2 e^{3x} $$
-
$$ y = C_1 + C_2 e^{4x} + C_3 e^{-3x} $$
-
(i) $$ y = C_1 e^x + C_2 e^{3x} + C_3 e^{-4x} $$
AI-generated content may contain errors. Please verify critical information