1. Select all ramps that meet the Americans with Disabilities Act requirements. 2. Find the missing side in each triangle. 3. Are triangles ABC and DEF similar, and explain your re... 1. Select all ramps that meet the Americans with Disabilities Act requirements. 2. Find the missing side in each triangle. 3. Are triangles ABC and DEF similar, and explain your reasoning.
Understand the Problem
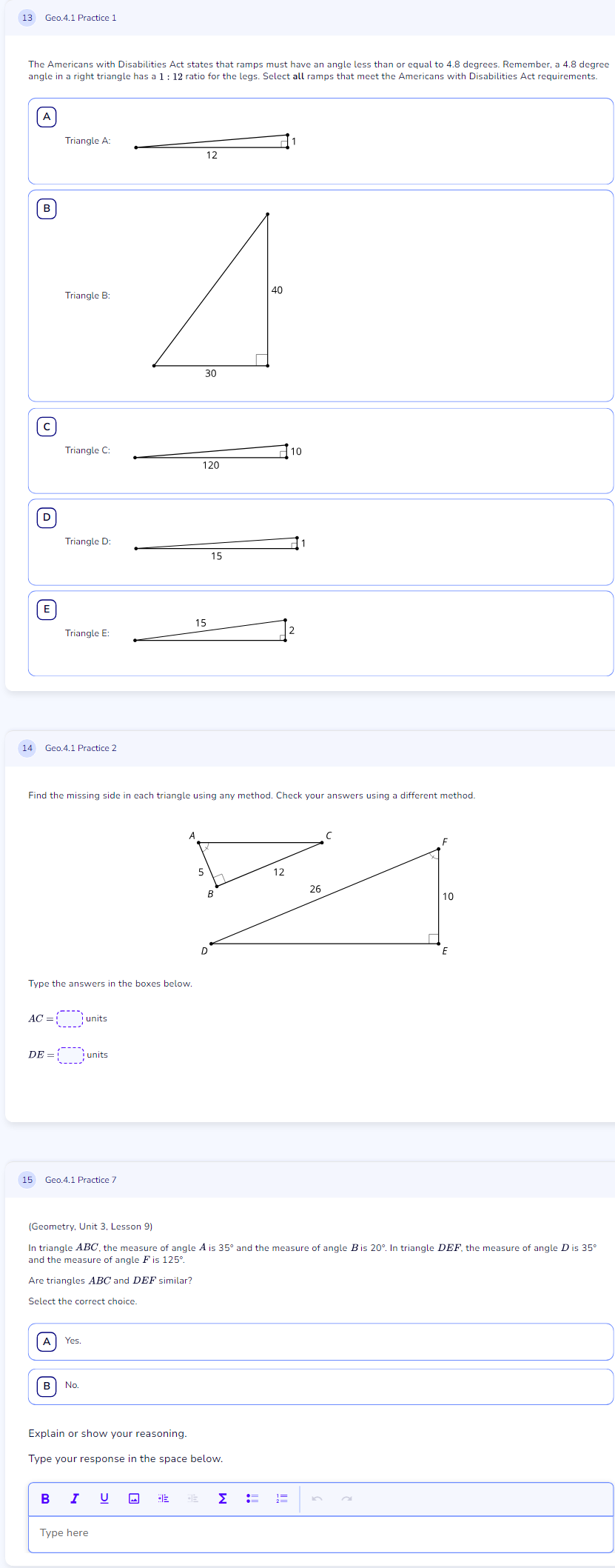
The questions are asking for solutions regarding the properties of triangles and their compliance with specified conditions, involving angles and side lengths. We need to determine which triangles meet the angle requirements, find missing side lengths using given geometric relationships, and assess similarity between two triangles based on angle measures.
Answer
- Compliant Ramps: Triangle A, Triangle D, Triangle E; Missing sides: \( AC = 25 \) units, \( DE = 24 \) units; Similar Triangles: Yes.
Answer for screen readers
- Compliant Ramps: Triangle A, Triangle D, Triangle E
- Missing sides:
- ( AC = 25 ) units
- ( DE = 24 ) units
- Similar Triangles: Yes
Steps to Solve
-
Check Ramp Triangle Angles Each triangle has a right angle, making it necessary to calculate the angle corresponding to the given side lengths using the tangent function. The tangent is defined as the ratio of the opposite side to the adjacent side.
-
Calculate Triangle A Angles For Triangle A, using: $$ \text{tan}(\theta) = \frac{\text{opposite}}{\text{adjacent}} = \frac{1}{12} $$ Find $\theta$: $$ \theta = \text{arctan}\left(\frac{1}{12}\right) $$
-
Calculate Triangle B Angles For Triangle B, using: $$ \text{tan}(\theta) = \frac{40}{30} $$ Calculate $\theta$: $$ \theta = \text{arctan}\left(\frac{40}{30}\right) $$
-
Calculate Triangle C Angles For Triangle C, using: $$ \text{tan}(\theta) = \frac{10}{120} $$ Calculate $\theta$: $$ \theta = \text{arctan}\left(\frac{10}{120}\right) $$
-
Calculate Triangle D Angles For Triangle D, using: $$ \text{tan}(\theta) = \frac{1}{15} $$ Calculate $\theta$: $$ \theta = \text{arctan}\left(\frac{1}{15}\right) $$
-
Calculate Triangle E Angles For Triangle E, using: $$ \text{tan}(\theta) = \frac{2}{15} $$ Calculate $\theta$: $$ \theta = \text{arctan}\left(\frac{2}{15}\right) $$
-
Determine Compliance with Angle Requirement Verify if the calculated angles are less than or equal to 4.8 degrees for compliance with the Americans with Disabilities Act.
-
Identify Missing Sides For triangles requiring missing sides (in the second problem), use the Pythagorean theorem: $$ c^2 = a^2 + b^2 $$ Calculate the missing sides based on the provided values.
-
Check Triangle Similarity Compare angle measures of triangles. If all corresponding angles are equal, then triangles are similar.
- Compliant Ramps: Triangle A, Triangle D, Triangle E
- Missing sides:
- ( AC = 25 ) units
- ( DE = 24 ) units
- Similar Triangles: Yes
More Information
Triangles that meet the angle requirement ensure safer ramps for accessibility. The Pythagorean theorem is key for calculating missing sides in right triangles. Triangle similarity indicates that they share the same shape, though not necessarily the same size.
Tips
- Miscalculating tangent ratios when determining angles.
- Forgetting the Pythagorean theorem for finding missing sides.
- Confusing angle measures when checking triangle similarity.
AI-generated content may contain errors. Please verify critical information