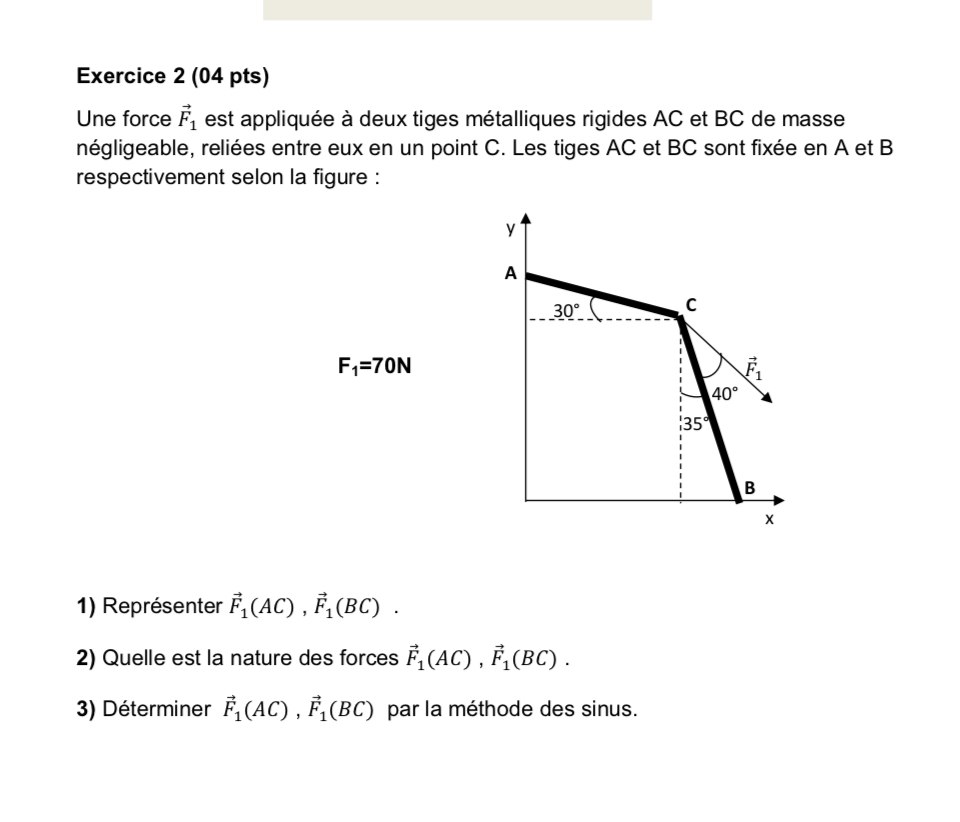
1) Représenter F1(AC), F1(BC). 2) Quelle est la nature des forces F1(AC), F1(BC). 3) Déterminer F1(AC), F1(BC) par la méthode des sinus.

Steps to Solve

1. Représentation des forces Il faut représenter les forces agissant sur les tiges AC et BC. Nous avons une force $F_1 = 70 , N$ appliquée à l'angle de 40° avec la tige BC. La force $F_1$ va se décomposer en deux composantes : $F_1(AC)$ et $F_1(BC)$.

2. Détermination des angles Pour déterminer les angles des forces, nous avons :

   • L'angle entre $F_1$ et $AC$ est $40°$.
   • L'angle de la tige AC avec l'horizontale est $(90° - 30°) = 60°$.
   • L'angle entre $F_1$ et $BC$ est $30°$.

3. Utilisation de la méthode des sinus Pour appliquer la méthode des sinus, nous allons établir un triangle où nous pouvons utiliser les angles donnés pour trouver les forces. Les angles des tiges sont respectivement de $30°$ et $35°$.

4. Application du théorème des sinus Nous savons que : $$ \frac{F_1(AC)}{\sin(35°)} = \frac{F_1(BC)}{\sin(30°)} = \frac{70 , N}{\sin(40°)} $$

5. Calcul des forces En utilisant les relations précédentes :

   • Pour $F_1(AC)$ : $$ F_1(AC) = \frac{70 , N \cdot \sin(35°)}{\sin(40°)} $$

   • Pour $F_1(BC)$ : $$ F_1(BC) = \frac{70 , N \cdot \sin(30°)}{\sin(40°)} $$

6. Calcul numérique Enfin, nous calculons numériquement les valeurs pour $F_1(AC)$ et $F_1(BC)$ en remplaçant les valeurs.