1. Find the Taylor's series expansion of: f(x, y) = x^3 + xy^2 about point (2, 1). 2. Find the first six terms of the expansions of the function e^x log(1 + y) in a neighbourhood o... 1. Find the Taylor's series expansion of: f(x, y) = x^3 + xy^2 about point (2, 1). 2. Find the first six terms of the expansions of the function e^x log(1 + y) in a neighbourhood of the point (0, 0). 3. Prove that a^x = 1 + x log a + (x^2 / 2!) (log a)^2 + (x^2 / 3!) (log a)^3 + ...... 4. Expand x^2 y + 3y - 2 in powers of (x - 1) and (y + 2) using Taylor's Theorem. 5. Expand x^y in powers of (x - 1) and (y - 1) up to the third-degree terms and beyond.
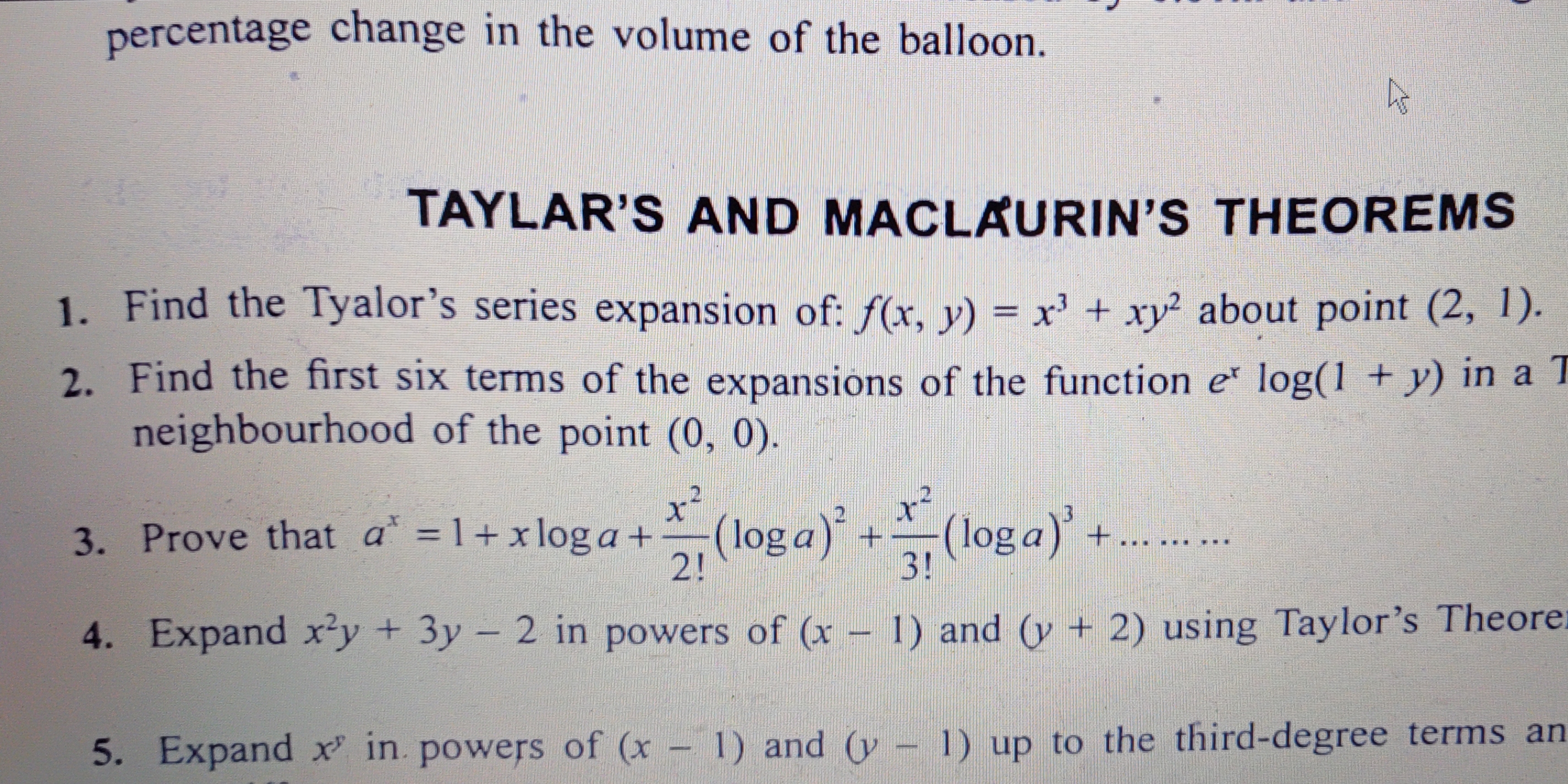
Understand the Problem
The question involves solving multiple problems related to Taylor's and Maclaurin's theorems, including finding series expansions and proving logarithmic relationships. The key concepts include Taylor series expansions, calculating terms, and expanding polynomials in different power series.
Answer
The Taylor series is $$ f(x, y) = 10 + 13(x - 2) + 4(y - 1) + 6(x - 2)^2 + 2(y - 1)^2 + 2(x - 2)(y - 1) + \ldots $$
Answer for screen readers
The Taylor series expansion of ( f(x, y) = x^3 + xy^2 ) about the point (2, 1) is:
$$ f(x, y) = 10 + 13(x - 2) + 4(y - 1) + 6(x - 2)^2 + 2(y - 1)^2 + 2(x - 2)(y - 1) + \ldots $$
Steps to Solve
- Find Partial Derivatives of f(x, y)
Calculate the first and second partial derivatives of the function ( f(x, y) = x^3 + xy^2 ):
- ( f_x = \frac{\partial f}{\partial x} = 3x^2 + y^2 )
- ( f_y = \frac{\partial f}{\partial y} = 2xy )
- ( f_{xx} = \frac{\partial^2 f}{\partial x^2} = 6x )
- ( f_{yy} = \frac{\partial^2 f}{\partial y^2} = 2x )
- ( f_{xy} = \frac{\partial^2 f}{\partial x \partial y} = 2y )
- Evaluate Derivatives at Point (2, 1)
Substitue ( x = 2 ) and ( y = 1 ) into the derivatives:
- ( f(2, 1) = 2^3 + 2 \cdot 1^2 = 8 + 2 = 10 )
- ( f_x(2, 1) = 3(2^2) + 1^2 = 12 + 1 = 13 )
- ( f_y(2, 1) = 2 \cdot 2 \cdot 1 = 4 )
- ( f_{xx}(2, 1) = 6 \cdot 2 = 12 )
- ( f_{yy}(2, 1) = 2 \cdot 2 = 4 )
- ( f_{xy}(2, 1) = 2 \cdot 1 = 2 )
- Formulate the Taylor Series Expansion
The Taylor series expansion of ( f(x, y) ) about the point (2, 1) is given by:
$$ f(x, y) = f(2, 1) + f_x(2, 1)(x - 2) + f_y(2, 1)(y - 1) + \frac{1}{2}f_{xx}(2, 1)(x - 2)^2 + \frac{1}{2}f_{yy}(2, 1)(y - 1)^2 + f_{xy}(2, 1)(x - 2)(y - 1) + \ldots $$
- Substitute Values into the Series
Substituting the evaluated values into the series gives:
$$ f(x, y) = 10 + 13(x - 2) + 4(y - 1) + \frac{1}{2}(12)(x - 2)^2 + \frac{1}{2}(4)(y - 1)^2 + (2)(x - 2)(y - 1) + \ldots $$
- Combine and Simplify the Series
Combine the terms in the series:
$$ f(x, y) = 10 + 13(x - 2) + 4(y - 1) + 6(x - 2)^2 + 2(y - 1)^2 + 2(x - 2)(y - 1) + \ldots $$
- First Six Terms of e^x log(1 + y) Expansion
The first six terms of the expansion can be derived by taking the Taylor series expansions of ( e^x ) and ( \log(1 + y) ), then combining:
- ( e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots )
- ( \log(1 + y) = y - \frac{y^2}{2} + \frac{y^3}{3} - \ldots )
- Combine these together for the undetermined terms.
- Expand a^x as Series
Using the definition of exponential and logarithm, begin from:
$$ a^x = e^{x \log a} = 1 + x \log a + \frac{x^2}{2!} (\log a)^2 + \frac{x^3}{3!} (\log a)^3 + \ldots $$
- Expand x^2y + 3y - 2
Use Taylor’s Theorem to expand about ( (1, -2) ):
-
Identify values based on calculated derivatives at that point.
-
Form and simplify the series representation.
-
Expand x^y
Utilize the logarithmic expansion similar to Step 7 and match it with expansions involving powers of ( (x - 1) ) and ( (y - 1) ).
The Taylor series expansion of ( f(x, y) = x^3 + xy^2 ) about the point (2, 1) is:
$$ f(x, y) = 10 + 13(x - 2) + 4(y - 1) + 6(x - 2)^2 + 2(y - 1)^2 + 2(x - 2)(y - 1) + \ldots $$
More Information
The Taylor series expansion helps approximate a function by using its derivatives at a specific point, making it easier to analyze complex functions. Taylor and Maclaurin series are widely used in calculus and physics for simplifying calculations and modeling.
Tips
- Forgetting to evaluate derivatives at the specified point.
- Not incorporating cross-derivative terms in multivariable Taylor expansions.
- Mismanaging terms when substituting values into the Taylor series.
AI-generated content may contain errors. Please verify critical information