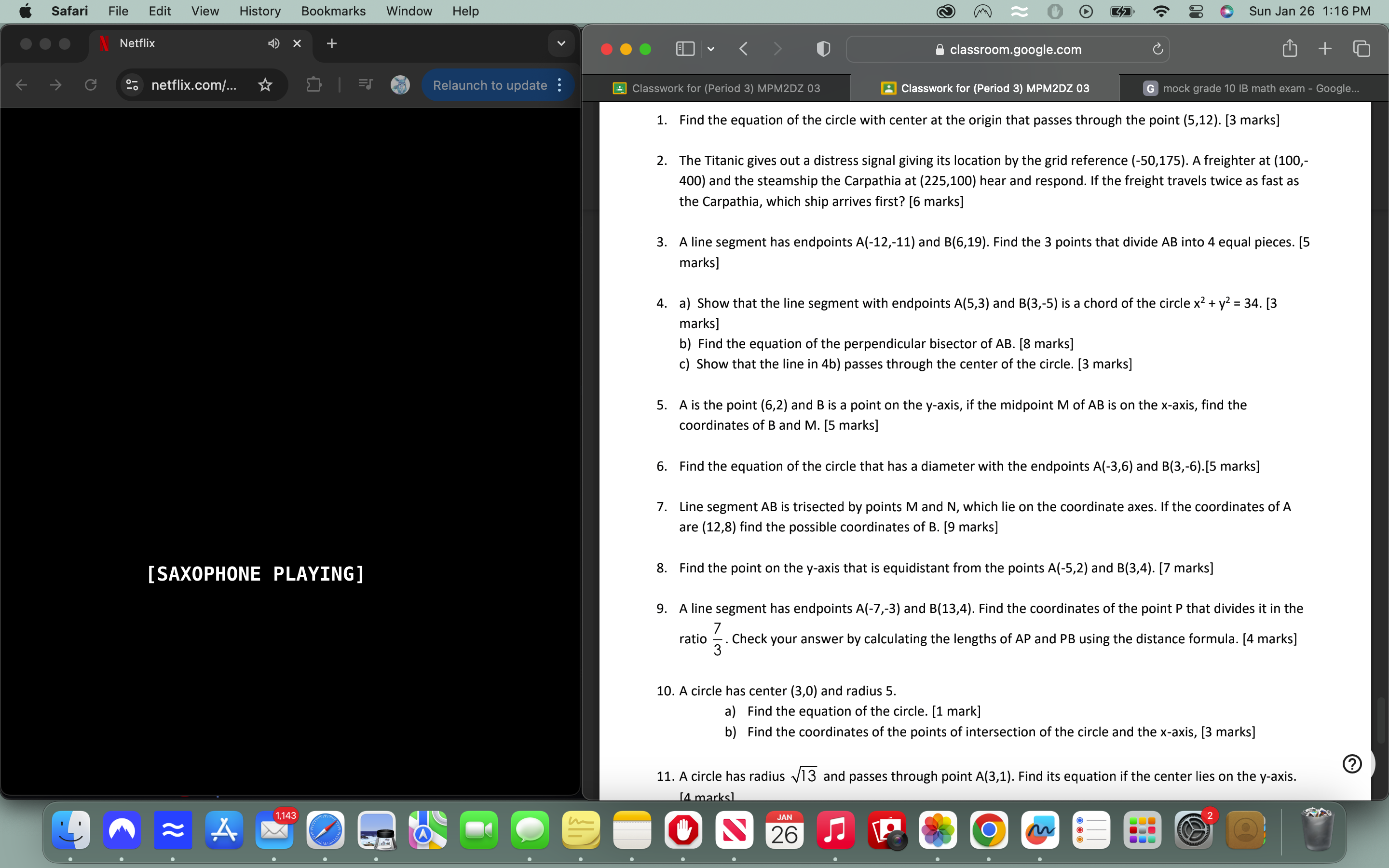
1. Find the equation of the circle with center at the origin that passes through the point (5,12). 2. The Titanic gives out a distress signal giving its location by the grid refere... 1. Find the equation of the circle with center at the origin that passes through the point (5,12). 2. The Titanic gives out a distress signal giving its location by the grid reference (-50,175). A freighter at (100,-400) and the steamship Carpathia at (225,100) hear and respond. If the freight travels twice as fast as Carpathia, which ship arrives first? 3. A line segment has endpoints A(-12,-11) and B(6,19). Find the 3 points that divide AB into 4 equal pieces. 4. a) Show that the line segment with endpoints A(5,3) and B(3,-5) is a chord of the circle x² + y² = 34. b) Find the equation of the perpendicular bisector of AB. c) Show that the line in 4b passes through the center of the circle. 5. A is the point (6,2) and B is a point on the y-axis; if the midpoint M of AB is on the x-axis, find the coordinates of B and M. 6. Find the equation of the circle that has a diameter with the endpoints A(-3,6) and B(3,-6). 7. Line segment AB is trisected by points M and N, which lie on the coordinate axes. If the coordinates of A are (12,8) find the possible coordinates of B. 8. Find the point on the y-axis that is equidistant from the points A(-5,2) and B(3,4). 9. A line segment has endpoints A(-7,-3) and B(13,4). Find the coordinates of the point P that divides it in the ratio 7:3. Check your answer by calculating the lengths of AP and PB using the distance formula. 10. A circle has center (3,0) and radius 5. a) Find the equation of the circle. b) Find the coordinates of the points of intersection of the circle and the x-axis. 11. A circle has radius √13 and passes through point A(3,1). Find its equation if the center lies on the y-axis.
Understand the Problem
The question is a set of geometry and algebra problems related to circles, line segments, and points on a Cartesian plane. It requires finding equations, coordinates, and demonstrating understanding of geometric properties.
Answer
The equation of the circle is \( x^2 + y^2 = 169 \).
Answer for screen readers
The equation of the circle is ( x^2 + y^2 = 169 ).
Steps to Solve
-
Identifying the problem
First, we need to find the equation of the circle with a radius equal to the distance from the origin to the point (5, 12). The general equation of a circle centered at the origin is given by:
$$ x^2 + y^2 = r^2 $$
where ( r ) is the radius. -
Calculating the radius
The radius is the distance from the origin (0,0) to the point (5,12). We can calculate this using the distance formula:
$$ r = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
Substituting in the values gives:
$$ r = \sqrt{(5-0)^2 + (12-0)^2} = \sqrt{25 + 144} = \sqrt{169} = 13 $$ -
Equation of the circle
Now that we have the radius, we substitute it back into the equation of the circle:
$$ x^2 + y^2 = 13^2 $$
This simplifies to:
$$ x^2 + y^2 = 169 $$
The equation of the circle is ( x^2 + y^2 = 169 ).
More Information
The equation represents a circle centered at the origin (0, 0) with a radius of 13. This kind of problem is common in geometry and helps visualize relationships between points and circles in a Cartesian plane.
Tips
- Forgetting to calculate the radius correctly using the distance formula.
- Mixing up the values when substituting into the circle equation.
AI-generated content may contain errors. Please verify critical information