∫(1 + 3x)x² dx
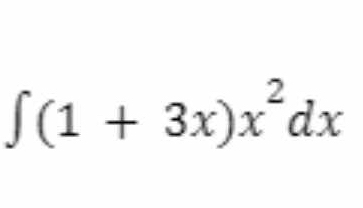
Understand the Problem
The question is asking to find the integral of the expression (1 + 3x)x² with respect to x. This involves applying techniques of integration to solve the problem.
Answer
$$\frac{x^3}{3} + \frac{3x^4}{4} + C$$
Answer for screen readers
The final answer is:
$$\frac{x^3}{3} + \frac{3x^4}{4} + C$$
Steps to Solve
- Expand the expression
First, we need to expand the integrand $(1 + 3x)x^2$:
$$(1 + 3x)x^2 = x^2 + 3x^3$$
- Set up the integral
Now we can rewrite our integral with the expanded expression:
$$\int (x^2 + 3x^3) , dx$$
- Integrate each term
We'll integrate each term separately:
- For $x^2$, the integral is:
$$\int x^2 , dx = \frac{x^{2+1}}{2+1} = \frac{x^3}{3}$$
- For $3x^3$, the integral is:
$$\int 3x^3 , dx = 3 \cdot \frac{x^{3+1}}{3+1} = \frac{3x^4}{4}$$
- Combine the results
Now, combine the results from the integrations:
$$\int (x^2 + 3x^3) , dx = \frac{x^3}{3} + \frac{3x^4}{4} + C$$
where $C$ is the constant of integration.
The final answer is:
$$\frac{x^3}{3} + \frac{3x^4}{4} + C$$
More Information
This result can be contextualized in the study of calculus, particularly in the application of the power rule of integration. The power rule is fundamental for integrating polynomials, allowing quick calculation of areas under curves defined by polynomial functions.
Tips
- Neglecting to distribute the terms correctly when expanding the expression.
- Forgetting to add the constant of integration $C$ at the end of the solution.
- Incorrectly applying the power rule by failing to adjust the exponent properly.
AI-generated content may contain errors. Please verify critical information