∫(1 + 3x)x² dx
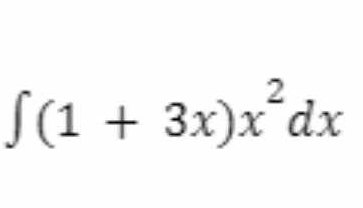
Understand the Problem
The question is asking us to compute the integral of the expression (1 + 3x)x² with respect to x. This involves using techniques of integration, likely polynomial expansion and then applying the power rule for integration.
Answer
$$ \frac{x^3}{3} + \frac{3x^4}{4} + C $$
Answer for screen readers
The final answer is: $$ \frac{x^3}{3} + \frac{3x^4}{4} + C $$
Steps to Solve
-
Expand the Expression Expand the expression $(1 + 3x)x^2$ using the distributive property. [ (1 + 3x)x^2 = x^2 + 3x^3 ]
-
Set Up the Integral Now, set up the integral to be evaluated: [ \int (x^2 + 3x^3) , dx ]
-
Apply the Power Rule Use the power rule for integration, which states that $\int x^n , dx = \frac{x^{n+1}}{n+1} + C$ for any real number $n \neq -1$.
First, integrate $x^2$: [ \int x^2 , dx = \frac{x^{3}}{3} ]
Next, integrate $3x^3$: [ \int 3x^3 , dx = 3 \cdot \frac{x^{4}}{4} = \frac{3x^{4}}{4} ]
- Combine the Results Combine the results from the integrals: [ \int (x^2 + 3x^3) , dx = \frac{x^3}{3} + \frac{3x^4}{4} + C ]
The final answer is: $$ \frac{x^3}{3} + \frac{3x^4}{4} + C $$
More Information
In this integral, we used the power rule, which simplifies the process of integrating polynomial terms. The constant of integration, $C$, is included because the process results in a family of functions (antiderivatives).
Tips
- Forgetting to include the constant of integration $C$ at the end of the integral.
- Misapplying the power rule, particularly confusing the coefficients during integration.
AI-generated content may contain errors. Please verify critical information