(1 1) . (x1) = (3) ( -1 1) (x2) (1)
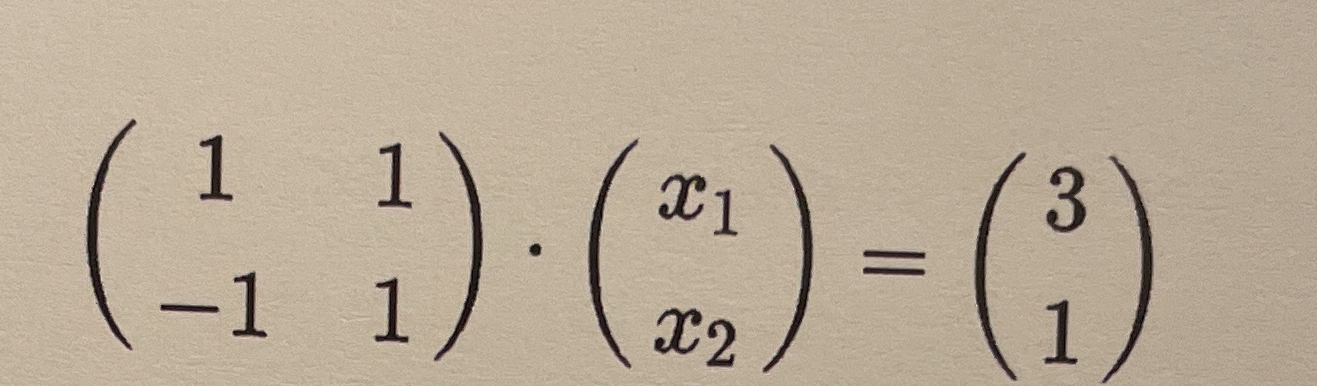
Understand the Problem
The question is asking to solve the matrix equation given on the left side and find the values of x1 and x2 such that the resulting vector equals the right-hand side vector. This can be accomplished by performing matrix multiplication and setting up a system of equations.
Answer
The values are \(x_1 = 1\) and \(x_2 = 2\).
Answer for screen readers
The values are (x_1 = 1) and (x_2 = 2).
Steps to Solve
-
Set Up the Matrix Equation
We begin by writing the matrix multiplication in equation form with the left-hand side matrix and the variable vector. We have: $$ \begin{pmatrix} 1 & 1 \ -1 & 1 \end{pmatrix} \begin{pmatrix} x_1 \ x_2 \end{pmatrix}\begin{pmatrix} 3 \ 1 \end{pmatrix} $$
-
Perform Matrix Multiplication
Now, we perform the dot product for each row of the left side:-
For the first row: $$ 1 \cdot x_1 + 1 \cdot x_2 = 3 $$
-
For the second row: $$ -1 \cdot x_1 + 1 \cdot x_2 = 1 $$
-
-
Set Up the System of Equations
This gives us two equations to solve:- $x_1 + x_2 = 3$
- $-x_1 + x_2 = 1$
-
Solve the First Equation for (x_2)
From the first equation, we can express (x_2) in terms of (x_1): $$ x_2 = 3 - x_1 $$ -
Substitute (x_2) into the Second Equation
Substitute (x_2) into the second equation: $$ -x_1 + (3 - x_1) = 1 $$ -
Combine Like Terms and Solve for (x_1)
This simplifies to: $$ -2x_1 + 3 = 1 $$ Rearrange to find (x_1): $$ -2x_1 = 1 - 3 \ -2x_1 = -2 \ x_1 = 1 $$ -
Find (x_2) Using (x_1)
Substitute (x_1) back to find (x_2): $$ x_2 = 3 - 1 = 2 $$
The values are (x_1 = 1) and (x_2 = 2).
More Information
The solution method involves applying matrix multiplication and solving a system of linear equations, which is common in linear algebra. These skills are vital in various applications, from computer graphics to data analysis.
Tips
- Ignoring the signs: When solving equations, be careful with negative signs, especially in the second equation.
- Forgetting to substitute back: After finding one variable, ensure you substitute it back correctly to find the other.
AI-generated content may contain errors. Please verify critical information