( ( 1 1 ) ( -1 1 ) ) · ( ( x1 ) ) = ( ( 3 ) ( 1 ) )

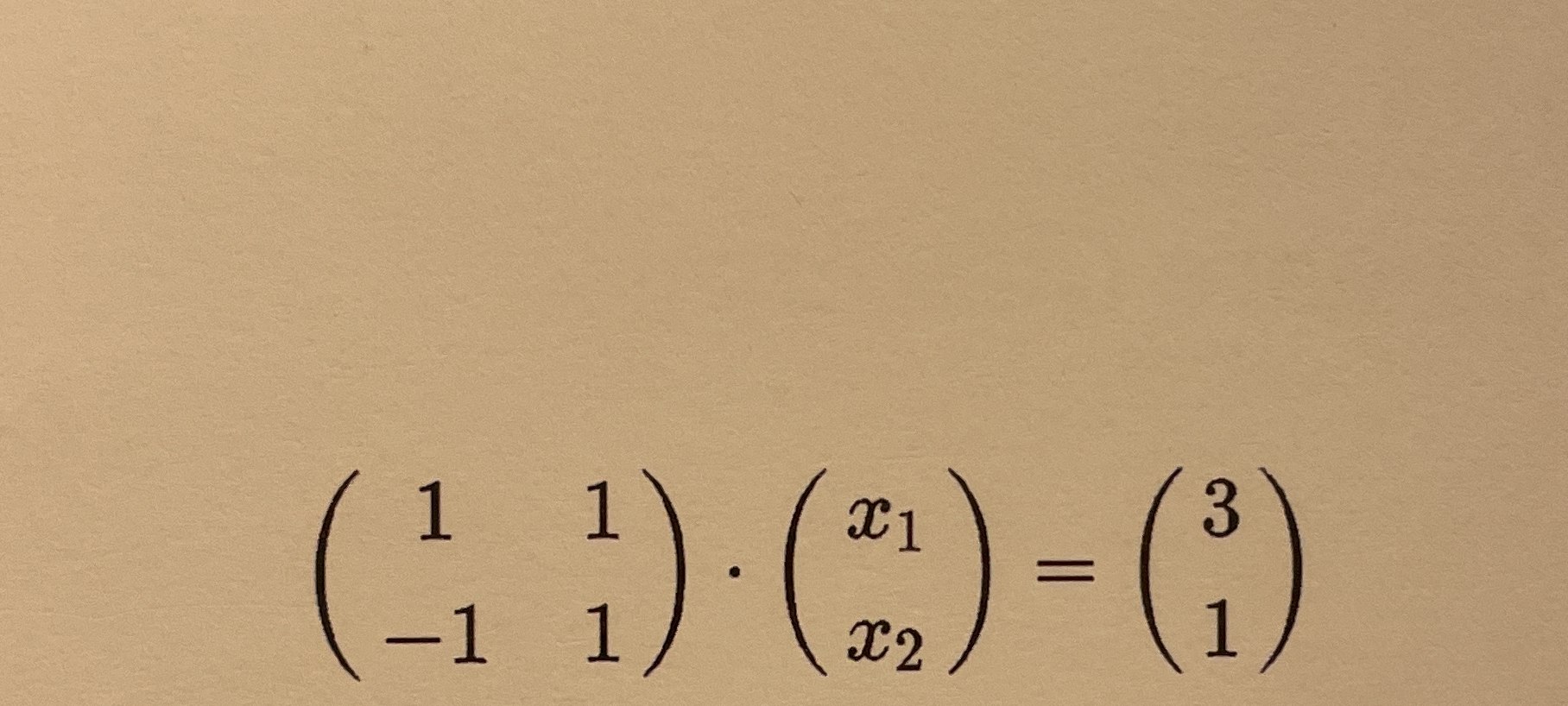
Understand the Problem

The question is asking to solve the matrix equation given, which involves multiplying a 2x2 matrix by a 2x1 vector, and equating it to another 2x1 vector. The goal is to find the values of x1 and x2.

Answer

The solution is $x_1 = 1$ and $x_2 = 2$.

Steps to Solve

Set up the equation We start with the equation given by multiplying the matrix and the vector: $$ \begin{pmatrix} 1 & 1 \ -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} x_1 \ x_2 \end{pmatrix} = \begin{pmatrix} 3 \ 1 \end{pmatrix} $$
Multiply the matrix by the vector To find the resulting vector, we perform the matrix multiplication:

The first row gives: $1 \cdot x_1 + 1 \cdot x_2 = 3$
The second row gives: $-1 \cdot x_1 + 1 \cdot x_2 = 1$

Set up the system of equations From the above calculations, we have two equations:
$x_1 + x_2 = 3$ (Equation 1)
$-x_1 + x_2 = 1$ (Equation 2)
Solve Equation 1 for $x_2$ Reorganizing Equation 1 gives us: $$ x_2 = 3 - x_1 \quad (\text{Substituting this in Equation 2}) $$
Substitute into Equation 2 Substitute $x_2$ in Equation 2: $$ -x_1 + (3 - x_1) = 1 $$ This simplifies to: $$ -2x_1 + 3 = 1 $$
Solve for $x_1$ Rearranging gives: $$ -2x_1 = 1 - 3 \implies -2x_1 = -2 \implies x_1 = 1 $$
Substitute $x_1$ back to find $x_2$ Using the value of $x_1$ to find $x_2$: $$ x_2 = 3 - 1 = 2 $$

The solution is: $$ x_1 = 1, \quad x_2 = 2 $$

More Information

This matrix equation and its solution demonstrate how to use matrix multiplication to represent systems of equations. The solution reveals the values of (x_1) and (x_2) that satisfy both equations derived from the matrix multiplication.

Tips

Not correctly performing matrix multiplication: Ensure you multiply the corresponding elements correctly.
Mistaking subtraction signs: Be careful when dealing with negative signs, especially in the second equation.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!