Statistics Chapter 10 & 13 - Correlation Analysis

Podcast

Play an AI-generated podcast conversation about this lesson

Questions and Answers

What is the concept of a linear relationship between paired quantitative data?

A linear relationship between paired quantitative data exists when the data points on a scatterplot tend to form a straight line.

What is the role of a scatter plot when analyzing paired data?

A scatter plot helps to assess whether a linear relationship exists and determines its direction, indicating a positive, negative, or no correlation.

What are the two coefficients commonly used to analyze linear correlation?

Spearman coefficient and Fisher coefficient

Karl-Pearson coefficient and Spearman coefficient (correct)

Karl-Pearson coefficient and Kendall coefficient

Fisher coefficient and Kendall coefficient

What is the coefficient of determination?

The coefficient of determination, represented by r², quantifies the proportion of the variation in one variable (y) explained by the linear relationship with another variable (x). Signup and view all the answers

What is the essence of paired data?

Paired data involves two sets of quantitative data linked together, representing measurements or observations for the same individuals or objects. Signup and view all the answers

Describe the core principle of correlation.

Correlation signifies the existence of a relationship between two variables, where one variable changes in a consistent manner with another variable. Signup and view all the answers

Define a scatterplot in terms of data representation.

A scatterplot is a graphical representation of paired data points (x, y), plotted on a coordinate plane with horizontal x-axis and vertical y-axis, where each point represents an individual observation or measurement. Signup and view all the answers

What does the linear correlation coefficient 'r' measure?

The linear correlation coefficient 'r' quantifies the strength of the linear relationship between paired x and y values within a sample, indicating the degree of association between the variables. Signup and view all the answers

What are the two assumptions associated with the linear correlation coefficient 'r'?

The sample of paired data (x, y) must be a random sample, and the pairs of data should exhibit a bivariate normal distribution. Signup and view all the answers

Explain the three main advantages of using rank correlation.

First, it is applicable in a wider range of situations compared to linear correlation. Second, it can identify some non-linear relationships. Third, its computations are simpler than those for linear correlation, facilitating analysis. Signup and view all the answers

What is the primary disadvantage of using Rank Correlation, and how does it affect its application?

The primary disadvantage of rank correlation is its lower efficiency compared to linear correlation, as reflected by its efficiency rating of 0.91. This suggests that rank correlation might require a larger sample size for achieving similar levels of precision compared to linear correlation. Signup and view all the answers

What is the central concept of rank correlation?

Rank correlation utilizes the rankings of sample data consisting of matched pairs to assess the association between two variables. Signup and view all the answers

What is the purpose of the rank correlation test?

The rank correlation test is employed to determine if a significant association exists between two variables, making it a valuable tool for exploring relationships when data is ranked or can be converted to ranks. Signup and view all the answers

What are the null and alternative hypotheses in rank correlation?

The null hypothesis (H0) states that there is no correlation between the two variables (ρs=0), whereas the alternative hypothesis (H1) suggests that a correlation exists between the variables (ρs≠0). Signup and view all the answers

What is the significance of 'rs' in rank correlation?

In rank correlation, 'rs' symbolizes the rank correlation coefficient for sample paired data, representing a sample statistic used to estimate the strength of the relationship between ranked variables. Signup and view all the answers

What is the difference between 'rs' and 'ρs' in rank correlation?

'rs' represents the rank correlation coefficient for a sample of paired data, while 'ρs' represents the rank correlation coefficient for the entire population from which the sample is drawn. Signup and view all the answers

What is the importance of the p-value in rank correlation?

The p-value in rank correlation determines the probability of obtaining the observed level of correlation if there were no association between the variables. A low p-value (typically less than 0.05) suggests strong evidence against the null hypothesis, indicating a significant relationship between the ranked variables. Signup and view all the answers

What is the most common error made when interpreting correlation?

A frequent error is to infer causation from correlation. Just because two variables exhibit a relationship does not automatically mean one causes the other. Correlation only demonstrates that they change consistently with each other, but there might be other underlying factors influencing both. Signup and view all the answers

Explain how averages affect correlation analysis, and what consequences can arise from misinterpreting this effect.

Averages can suppress individual variations within data, potentially exaggerating the correlation coefficient. This occurs because averages mask fluctuations and create a false impression of a stronger relationship than what truly exists in the underlying data. Misinterpreting the effect of averages can lead to inaccurate conclusions about the strength of relationships, potentially overestimating the significance of the association. Signup and view all the answers

What is the key point to remember about linearity in relation to correlation?

It's important to remember that the absence of a significant linear correlation does not automatically mean there is no relationship between variables. There might be a non-linear relationship present, meaning the variables change in a non-straight line pattern. Signup and view all the answers

Study Notes

Correlation and Rank Correlation

Correlation exists when one variable relates to another.
A scatter plot visualizes paired (x,y) data. Each point represents a pair.
The x-axis is horizontal.
The y-axis is vertical.

Lecture Objectives

Students will understand linear relationships in paired quantitative data.
Students will analyze scatter plots to identify linear relationships.
Students will conduct hypothesis tests to calculate and evaluate correlation coefficients (Pearson and Spearman) using JMP software.
Students will compute and interpret the coefficient of determination.
Refer to chapters 10 & 13, sections 10.1 and 13.6.

Paired Data Overview

Assess if a relationship exists.
Evaluate the strength of the relationship.

Correlation Definition

Correlation exists between two variables when one is related to the other in some way.

Scatterplot Definition

A scatterplot is a graph that shows paired (x, y) sample data plotted on a horizontal x-axis and a vertical y-axis.

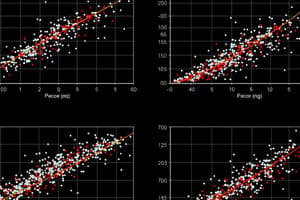
Scatter Diagram of Paired Data

The example shows data about manatee deaths versus registered boats.
The data is plotted in an x-y plane, representing the relationship between these two variables.

Scatter Plots Illustrating Different Correlation Structures

Illustrates examples of perfect positive correlation, perfect negative correlation, strong negative correlation, quadratic function, random values, and no correlation. Visually demonstrating different patterns.

JMP Example: Scatterplot

Examines blood sugar levels (Y) in relation to Body Mass Index (BMI) in the diabetes.jmp file.
Asks if there's a linear relationship between these variables.

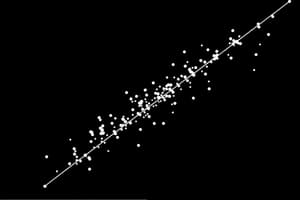
JMP Fit Y by X: Scatterplot

Shows a positive linear relationship between blood sugar levels and BMI.
The scatter plot displays many data points.

JMP Example: Scatterplot (Blood Pressure)

Data from fourteen students measures blood pressure in patients.
Examines correlation between systolic and diastolic blood pressures.

Linear Correlation Coefficient Definition

The coefficient (r) measures the strength of a linear relationship between paired x and y values in a sample.

Strength of Linear Relationship

Correlation coefficients quantify the strength of linear relationships.
Values above 0.8 are considered very strong, 0.6-0.8 moderately strong, 0.3-0.5 fair, and less than 0.3 poor.

Linear Correlation Coefficient Assumptions

The sample data (x, y) must be a random sample.
The (x, y) pairs should follow a bivariate normal distribution.

Linear Correlation Coefficient Notations

n denotes the number of data pairs.
Σ denotes summation of items.
Σx represents the sum of all x-values.
Σx² denotes the sum of squared x-values.
(Σx)² means the sum of x-values squared.
Σxy denotes the sum of the products of corresponding x and y values.
r is the sample correlation coefficient.
ρ is the population correlation coefficient.

Example: Calculating r

Example data set (x,y) values to calculate the correlation coefficient (r).

Calculating r

Shows the formula and calculation steps for calculating the correlation coefficient.

Linear Correlation Coefficient Properties

The correlation coefficient (r) always falls between -1 and +1.
The value of r doesn't change if the variable values are scaled differently.
The choice of x or y doesn't affect the correlation value.
r measures the strength of the linear relationship between two variables.

Explained Variation Coefficient of Determination Interpreting

r² represents the proportion of the variation in y explained by the linear relationship with x.
r² is the coefficient of determination.

Example for r²: Boats and Manatees

Using data from table 9-1, the linear correlation coefficient r is 0.922.
r² is 0.850, meaning 85% of the variation in manatee deaths can be attributed to the variation in boat registrations.

Linear Correlation Coefficient Formal Hypothesis Testing

Null Hypothesis (H₀): ρ = 0 (no significant linear correlation)
Alternative Hypothesis (H₁): ρ ≠ 0 (significant linear correlation)

JMP Example: Pearson Linear Correlation

Analyze the relationship between variables Y and BMI using the diabetes.jmp dataset in JMP.

JMP Output: Pearson Correlation

Calculates the Pearson correlation coefficient (r) and the p-value. Example coefficient and p-values are provided.

Interpretation: Pearson Linear Correlation

Defines the strength, direction, and significance of the linear correlation between Y and BMI.

Rank Correlation Definition

Rank correlation uses the ranks of sample data, not the actual values.
This version assesses associations between variables, whether linear or non-linear.

Rank Correlation Advantages

Can be used in more diverse situations than parametric methods.
Can analyze paired data expressed as ranks or convertible to ranks.
Can detect non-linear relationships.
Computational simplicity compared to parametric correlation.

Rank Correlation Disadvantages

Lower efficiency (0.91) than parametric methods.

Rank Correlation Notations

r_s is the sample rank correlation coefficient.
ρ_s is the population rank correlation coefficient.
n is the number of data pairs.

JMP Example: Spearman's Rank Correlation

Examines cotinine in the body as an indicator of smoking behavior.
Assesses correlation between cigarettes per day and cotinine levels.

JMP Output: Spearman's Rank Correlation

Provides the Spearman correlation coefficient (r_s) and associated p-value.

Interpretation: Spearman's Rank Correlation

Summarizes the strength, direction, and significance of the Spearman's rank correlation.

Common Errors Involving Correlation

Causation: Correlation does not imply causality.
Averages: Averages can mask individual variation and potentially inflate correlation coefficients.
Non-linearity: A relationship might exist between x and y, but it may not be linear, even without a significant linear correlation.

Studying That Suits You

Use AI to generate personalized quizzes and flashcards to suit your learning preferences.

Description

This quiz focuses on understanding correlation and rank correlation in paired quantitative data. Students will analyze scatter plots and conduct hypothesis tests to evaluate correlation coefficients using JMP software. Key concepts from chapters 10 and 13 are covered, including the coefficient of determination.