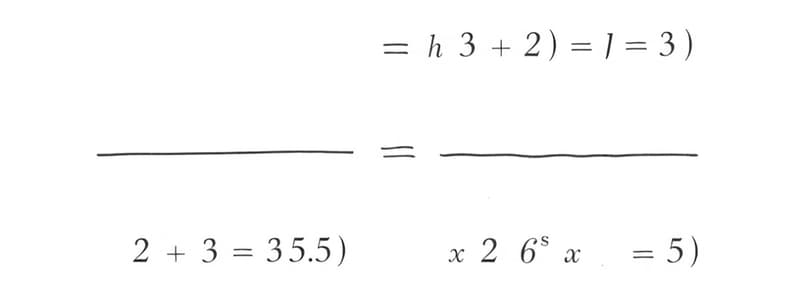Podcast
Questions and Answers
Qual è il valore della derivata della funzione $f(x)$ in $x = 0$?
Qual è il valore della derivata della funzione $f(x)$ in $x = 0$?
La derivata $f'(x)$ non esiste in $x = 0$.
Qual è la definizione della funzione segno $sgn(x)$ per $x > 0$?
Qual è la definizione della funzione segno $sgn(x)$ per $x > 0$?
$sgn(x) = +1$ per $x > 0$.
Cosa significa $se , x , = , 0$ in relazione alla funzione $sgn(x)$?
Cosa significa $se , x , = , 0$ in relazione alla funzione $sgn(x)$?
Quando $x = 0$, $sgn(x) = 0$.
Qual è il valore di $sgn(x)$ quando $x < 0$?
Qual è il valore di $sgn(x)$ quando $x < 0$?
Perché si afferma che $
exists se , x , = , 0$ nella definizione della derivata di $f(x)$?
Perché si afferma che $ exists se , x , = , 0$ nella definizione della derivata di $f(x)$?
Qual è la definizione della funzione modulo di un numero x?
Qual è la definizione della funzione modulo di un numero x?
Perché la funzione modulo è considerata una funzione pari?
Perché la funzione modulo è considerata una funzione pari?
Qual è il valore della funzione modulo per x = -5?
Qual è il valore della funzione modulo per x = -5?
Come si rappresenta graficamente la funzione f(x) = |x|?
Come si rappresenta graficamente la funzione f(x) = |x|?
Qual è la derivata della funzione f(x) = |x| per x ≠ 0?
Qual è la derivata della funzione f(x) = |x| per x ≠ 0?
Cosa rappresenta il valore assoluto in termini di distanza?
Cosa rappresenta il valore assoluto in termini di distanza?
Qual è l'equazione della funzione modulo quando x è uguale a zero?
Qual è l'equazione della funzione modulo quando x è uguale a zero?
Come si descrive il comportamento della funzione modulo per valori molto grandi di x?
Come si descrive il comportamento della funzione modulo per valori molto grandi di x?
Qual è la definizione della funzione $sgn(x)$ quando $x = 0$?
Qual è la definizione della funzione $sgn(x)$ quando $x = 0$?
Qual è il valore di $sgn(x)$ per $x < 0$?
Qual è il valore di $sgn(x)$ per $x < 0$?
Spiega perché la funzione $f(x) = |x|$ non è derivabile in $x = 0$.
Spiega perché la funzione $f(x) = |x|$ non è derivabile in $x = 0$.
Qual è l'espressione della funzione $f'(x)$ quando $x
eq 0$ per la funzione valore assoluto?
Qual è l'espressione della funzione $f'(x)$ quando $x eq 0$ per la funzione valore assoluto?
Descrivi graficamente la funzione $f(x) = |x|$ per valori molto grandi di $x$.
Descrivi graficamente la funzione $f(x) = |x|$ per valori molto grandi di $x$.
Qual è l'espressione della funzione modulo per x negativo?
Qual è l'espressione della funzione modulo per x negativo?
Qual è l'andamento della funzione f(x) = |x| quando x è positivo?
Qual è l'andamento della funzione f(x) = |x| quando x è positivo?
Che proprietà ha la funzione modulo in relazione alla simmetria?
Che proprietà ha la funzione modulo in relazione alla simmetria?
Qual è il comportamento della funzione modulo per x uguale a zero?
Qual è il comportamento della funzione modulo per x uguale a zero?
Che significato hanno i valori della funzione f(x) = |x| in termini geometrici?
Che significato hanno i valori della funzione f(x) = |x| in termini geometrici?
Qual è la derivata della funzione f(x) = |x| in corrispondenza dei punti non nulli?
Qual è la derivata della funzione f(x) = |x| in corrispondenza dei punti non nulli?
Come si rappresenta graficamente la funzione f(x) = |x|?
Come si rappresenta graficamente la funzione f(x) = |x|?
Per quali valori di x l'equazione f(x) = |x| è definita?
Per quali valori di x l'equazione f(x) = |x| è definita?
Flashcards
Funzione modulo
Funzione modulo
Funzione che restituisce il valore assoluto di un numero.
sgn(x)
sgn(x)
Funzione segno, restituisce 1 se x > 0, -1 se x < 0 e 0 se x = 0.
Derivata |x| in x=0
Derivata |x| in x=0
La funzione valore assoluto non è derivabile in x=0.
Funzione modulo di x
Funzione modulo di x
Signup and view all the flashcards
Definizione di |x|
Definizione di |x|
Signup and view all the flashcards
Grafico di |x|
Grafico di |x|
Signup and view all the flashcards
Funzione pari
Funzione pari
Signup and view all the flashcards
Derivata di |x|
Derivata di |x|
Signup and view all the flashcards
Funzione modulo
Funzione modulo
Signup and view all the flashcards
sgn(x)
sgn(x)
Signup and view all the flashcards
Derivata |x| in x=0
Derivata |x| in x=0
Signup and view all the flashcards
|x| in x=0
|x| in x=0
Signup and view all the flashcards
grafico di |x|
grafico di |x|
Signup and view all the flashcards
Funzione Modulo
Funzione Modulo
Signup and view all the flashcards
Valore Assoluto di x
Valore Assoluto di x
Signup and view all the flashcards
Grafico di |x|
Grafico di |x|
Signup and view all the flashcards
|x| in x>0
|x| in x>0
Signup and view all the flashcards
|x| in x<0
|x| in x<0
Signup and view all the flashcards
|x| in x=0
|x| in x=0
Signup and view all the flashcards
Funzione Pari
Funzione Pari
Signup and view all the flashcards
Study Notes
Funzione Modulo
- La funzione modulo, nota anche come valore assoluto, è rappresentata da |x|.
- Se x è maggiore di 0, il risultato è x.
- Se x è uguale a 0, il risultato è 0.
- Se x è minore di 0, il risultato è -x.
Grafico della Funzione Modulo
- Il grafico è una linea retta a forma di "V" con il vertice nell'origine (0,0).
- La parte sinistra del grafico, per x minore di 0, è una semiretta decrescente.
- La parte destra del grafico, per x maggiore di 0, è una semiretta crescente.
- La funzione attraversa il punto (0,0)
- La funzione è sempre definita in R.
- La funzione è sempre positiva (il codominio è R+).
- La funzione passa attraverso il punto (0,0).
- La funzione è decrescente per x < 0 e crescente per x > 0.
- La funzione è una funzione pari.
- La funzione è composta da due semirette che formano un angolo di 180 gradi.
Proprietà della Funzione Modulo
- |a| ≥ 0
- |a|= 0 ⇔ a = 0
- |ab| = |a||b|
- |a|/|b| = |a|/|b| se b diverso da 0
- |a+b| ≤ |a| + |b|
- |a-b| ≥ ||a| - |b||
- |a-b|= 0 ⇔ a = b
- |a| ≤ b ⇔ -b ≤ a ≤ b
- |a| ≥ b ⇔ a ≤ -b V a ≥ b
Derivabilità della Funzione Modulo
-
La funzione modulo non è derivabile in x = 0.
-
La funzione ha una discontinuità sulla derivata primo a x = 0.
-
y' = f'(x) = ? Per x diverso da 0, f'(x) può essere espressa tramite la funzione segno sgn(x):
-
f'(x)= |x|/x = sgn(x), se x ≠0
-
sgn (x) = +1 se x > 0, 0 se x = 0, -1 se x < 0.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.