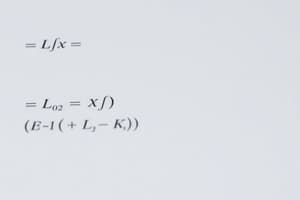Podcast
Questions and Answers
What is the first step to compute $99(2x - 198)^2 x - 99$ dx?
What is the first step to compute $99(2x - 198)^2 x - 99$ dx?
What is the volume of a square pyramid with base area $r^2$ and height $h$?
What is the volume of a square pyramid with base area $r^2$ and height $h$?
If $f$ is an integrable function on $[0,1]$, which statement is true about $|f|$?
If $f$ is an integrable function on $[0,1]$, which statement is true about $|f|$?
What does the well-ordering principle state?
What does the well-ordering principle state?
Signup and view all the answers
If $ ext{lim}{x o p^+} f(x) = ext{lim}{x o p^-} f(x) = A$, what can be concluded about $ ext{lim}_{x o p} f(x)$?
If $ ext{lim}{x o p^+} f(x) = ext{lim}{x o p^-} f(x) = A$, what can be concluded about $ ext{lim}_{x o p} f(x)$?
Signup and view all the answers
To find $(f^{-1})'(0)$ where $f(x) = rac{1}{2} ext{cos}( ext{sin} t)$, what must be known?
To find $(f^{-1})'(0)$ where $f(x) = rac{1}{2} ext{cos}( ext{sin} t)$, what must be known?
Signup and view all the answers
What can be concluded if a function $f(x)$ is continuous on $[0, 1]$ and $f(0) = f(1)$?
What can be concluded if a function $f(x)$ is continuous on $[0, 1]$ and $f(0) = f(1)$?
Signup and view all the answers
Which of the following properties is true for the function defined on $[-1, 1]$ that is continuous and differentiable but has a derivative that is not continuous?
Which of the following properties is true for the function defined on $[-1, 1]$ that is continuous and differentiable but has a derivative that is not continuous?
Signup and view all the answers
Flashcards
What is [x]?
What is [x]?
The largest integer less than or equal to x.
What is the volume of a square pyramid?
What is the volume of a square pyramid?
The volume of a pyramid is equal to one-third the product of its base area and height.
Integrability of |f(x)|
Integrability of |f(x)|
If f(x) is integrable on an interval, then its absolute value, |f(x)|, is also integrable on that interval.
Prove the principle of mathematical induction using the well-ordering principle.
Prove the principle of mathematical induction using the well-ordering principle.
Signup and view all the flashcards
Prove lim x→p f(x) = A if lim x→p+ f(x) = lim x→p- f(x) = A.
Prove lim x→p f(x) = A if lim x→p+ f(x) = lim x→p- f(x) = A.
Signup and view all the flashcards
How to find lim h→0 [F(a+h) - F(a)]/h ?
How to find lim h→0 [F(a+h) - F(a)]/h ?
Signup and view all the flashcards
Find the derivative of an inverse function.
Find the derivative of an inverse function.
Signup and view all the flashcards
Find f(2) given integrals of f(x) and f'(x).
Find f(2) given integrals of f(x) and f'(x).
Signup and view all the flashcards
Study Notes
Practice Exam 1
-
Problem 1: Calculate the definite integral $\int_{}^{} (2x - 198)^{2} [\sqrt{x} - 99] dx$. The function includes the greatest integer function.
-
Problem 2: Find the volume of the square pyramid using Cavalieri's theorem. The pyramid has a base area of $r^2$ and height $h$.
-
Problem 3: Prove that the absolute value $|f|$ of an integrable function $f$ on the interval [0,1] is also integrable.
-
Problem 4: Show that the well-ordering principle implies the principle of mathematical induction. This involves a set $S$ of natural numbers, and a subset $T$.
-
Problem 5: If the limit of a function $f(x)$ as $x$ approaches $p$ from the left and right both equal $A$, prove that the limit as $x$ approaches $p$ is also $A$.
Practice Exam 2
-
Problem 1: Evaluate the limit $\lim_{h\to0} \frac{\int_{0}^{1+h} e^{t^2} dt - \int_{0}^{1} e^{t^2} dt}{h(3+h^2)}$, using a theorem.
-
Problem 2: Find the derivative of the inverse function $(f^{-1})'(0)$, for a specific function $f(x)$ involving a definite integral.
-
Problem 3: Find the value of $f(2)$ given a definite integral equation. The function $f(x)$ is continuous.
-
Problem 4: Provide an example of a function $f(x)$ on the interval [-1,1] that is continuous and differentiable but whose derivative $f'(x)$ is not continuous at certain points.
-
Problem 5: Demonstrate that if $f(x)$ is continuous on [0,1] and $f(0)=f(1)$, then there exists a point $x\in[0,1]$ such that $f(x)=f(x+1/n)$ for any positive integer $n$.
Practice Exam 3
-
Problem 1: Evaluate the integral $\int_{}^{} \frac{t + t^2}{\sqrt{1 + t^2}} dt$
-
Problem 2: Calculate the integral $\int_{}^{} x^2 \sqrt{x^2 - 9} dx$
-
Problem 3: Given $\lim_{x→a^+} g(x) = B$ (a finite, non-zero value) and $\lim_{x→a^+} h(x) = 0$, with $h(x) \neq 0$ near $a$, prove that $\lim_{x→a^+} \frac{g(x)}{h(x)}$ is infinity.
-
Problem 4: If $f(x)$ is a positive continuous function on [0,$\infty$) with $\lim_{x→∞} f(x) = 0$, prove that there exists a maximum value $M$ for $f(x)$ on the interval [0, $\infty$).
-
Problem 5: Demonstrate that a convergent sequence is a Cauchy sequence. A function $f$ is a contraction if there exists 0 < a < 1 such that $|f(x) - f(y)| ≤ a|x-y|$. Show that if $f$ is a contraction in the composition of $f$ on itself $n$ times, the sequence formed is Cauchy.
Studying That Suits You
Use AI to generate personalized quizzes and flashcards to suit your learning preferences.
Related Documents
Description
This quiz covers various topics in calculus and analysis including definite integrals, volume calculations using Cavalieri's theorem, and principles of mathematical induction. It features complex problem-solving and proofs related to limits and integrability. Perfect for those preparing for advanced mathematics exams.
