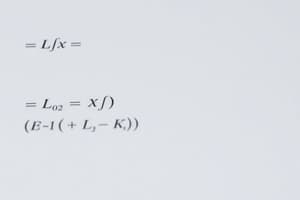Calculus Basics: Limits, Derivatives, Integrals, and Differentials

Study Notes

Calculus is a branch of mathematics that deals with continuous changes and rates of change. It involves studying limits, derivatives, integrals, and differentials. Here's some information on these key aspects of calculus:

Limits: A limit allows us to determine what happens to variables when they get very close together while still being distinct. For instance, if you have x going towards y, its limit could be considered zero. Limits are often used to define derivative functions.

Derivatives: In calculus, a function that gives us how fast something is changing over time, relative to another quantity is called a derivative. For example, consider the height of a sine wave over time; we might want to know how quickly it's growing or shrinking at any given moment. This would correspond to its first derivative, which tells us exactly where its peaks and troughs will occur along this curve.

Integrals: Integrals calculate the area under curves by taking small parts of them into account one after another until all areas between two points have been added up correctly. They can also represent accumulated values from past events, such as total costs or profits made during certain periods.

Differentials: If we give each point along a line segment a name so that we may refer back easily later on, those names become differential elements. Differential equations describe physical systems, like predicting speeds based on forces moving objects around paths determined by their velocities.

Calculus has numerous applications in fields beyond pure math itself - economics, physics, engineering, biology, and even philosophy rely heavily upon concepts derived from this discipline. So whether you're tracking stock market trends, designing bridges, understanding biological processes within living organisms, or pondering deep philosophical questions related to existence itself - understanding calculus can serve as an integral part of your journey!

Description

Learn about key aspects of calculus including limits, derivatives, integrals, and differentials. Understand how these concepts help in studying continuous changes, rates of change, and predicting behaviors of various functions and systems.