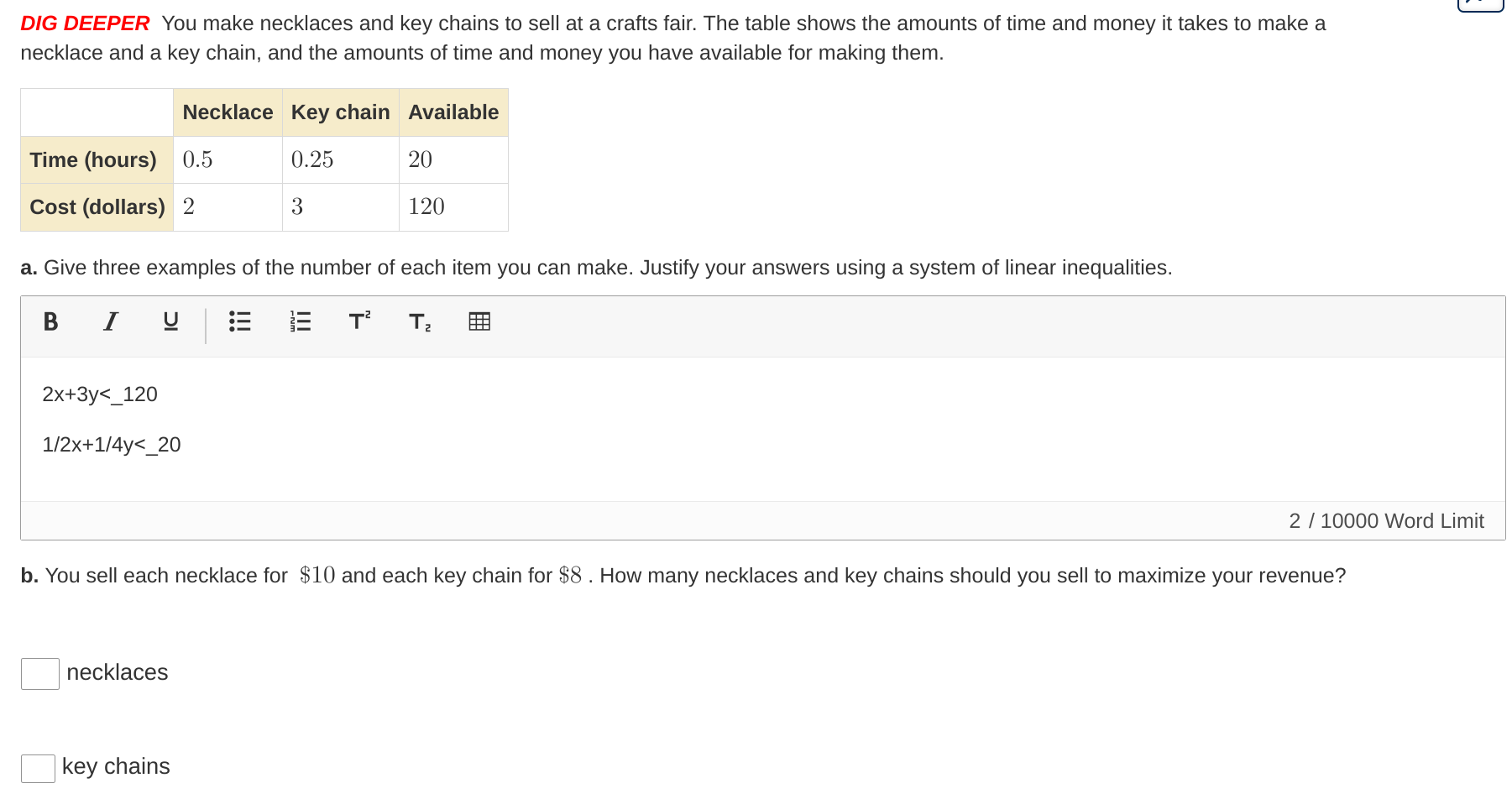
You make necklaces and key chains to sell at a crafts fair. The table shows the amounts of time and money it takes to make a necklace and a key chain, and the amounts of time and m... You make necklaces and key chains to sell at a crafts fair. The table shows the amounts of time and money it takes to make a necklace and a key chain, and the amounts of time and money you have available for making them. a. Give three examples of the number of each item you can make. Justify your answers using a system of linear inequalities. b. You sell each necklace for $10 and each key chain for $8. How many necklaces and key chains should you sell to maximize your revenue? Read more

Steps to Solve

1. Set Up Variables

Define the variables for the items being made:

• Let ( x ) = number of necklaces
• Let ( y ) = number of key chains

2. Establish Inequalities from Constraints

From the problem statement, create inequalities based on time and cost:

• Time Constraint: Each necklace takes 0.5 hours and each key chain takes 0.25 hours. Given a total of 20 hours:

  $$ 0.5x + 0.25y \leq 20 $$

• Cost Constraint: Each necklace costs $2 and each key chain costs $3. With $120 available:

  $$ 2x + 3y \leq 120 $$

3. Non-negativity Constraints

Since you cannot produce a negative number of items, add the constraints:

$$ x \geq 0 $$
$$ y \geq 0 $$

4. Example Combinations

Now, let's find three examples of ( (x, y) ):

• Example 1: If ( x = 20 ) and ( y = 0 ):
  $$ 0.5(20) + 0.25(0) = 10 \leq 20 $$ (Time)
  $$ 2(20) + 3(0) = 40 \leq 120 $$ (Cost)

• Example 2: If ( x = 10 ) and ( y = 20 ):
  $$ 0.5(10) + 0.25(20) = 5 + 5 = 10 \leq 20 $$ (Time)
  $$ 2(10) + 3(20) = 20 + 60 = 80 \leq 120 $$ (Cost)

• Example 3: If ( x = 5 ) and ( y = 30 ):
  $$ 0.5(5) + 0.25(30) = 2.5 + 7.5 = 10 \leq 20 $$ (Time)
  $$ 2(5) + 3(30) = 10 + 90 = 100 \leq 120 $$ (Cost)

5. Maximizing Revenue

You sell necklaces for $10 and key chains for $8. Define the revenue function:

$$ R = 10x + 8y $$

Now, use the constraints to find ( x ) and ( y ) that maximize ( R ) within the defined limits.