You deposit $750 in a savings account that earns 5% annual interest compounded quarterly. a. Write a function that represents the balance y (in dollars) after t years. b. What is t... You deposit $750 in a savings account that earns 5% annual interest compounded quarterly. a. Write a function that represents the balance y (in dollars) after t years. b. What is the balance of the account after 4 years?
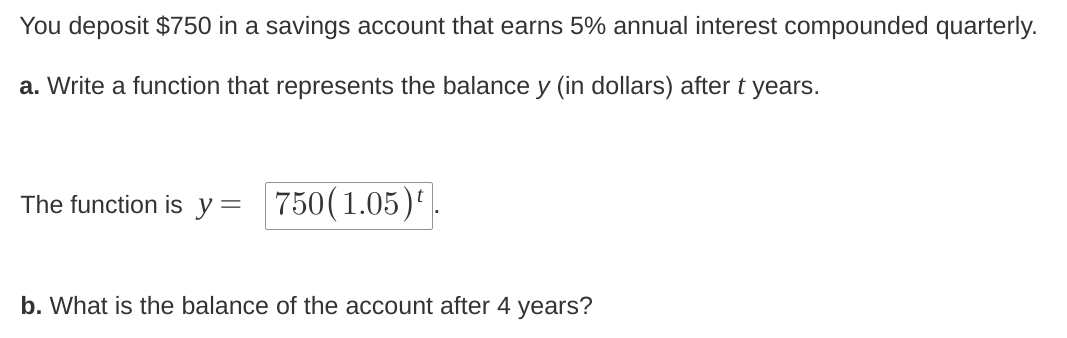
Understand the Problem
The question involves calculating the balance of a savings account that earns interest compounded quarterly. It asks for a function representing the balance over time and then specifically for the balance after 4 years.
Answer
The balance after 4 years is approximately $915.99.
Answer for screen readers
The balance of the account after 4 years is approximately $915.99.
Steps to Solve
- Identify the Compounding Interest Formula
To find the balance in a savings account that compounds interest, we use the formula:
$$ A = P \left(1 + \frac{r}{n}\right)^{nt} $$
where:
- ( A ) = the amount of money accumulated after n years, including interest.
- ( P ) = the principal amount (the initial amount of money).
- ( r ) = annual interest rate (decimal).
- ( n ) = number of times that interest is compounded per year.
- ( t ) = the number of years the money is invested or borrowed.
- Substitute Known Values into the Formula
Given:
- ( P = 750 )
- ( r = 0.05 )
- ( n = 4 ) (quarterly compounding)
- ( t = 4 )
Substituting these values in, we have:
$$ A = 750 \left(1 + \frac{0.05}{4}\right)^{4 \cdot t} $$
- Simplify the Equation
Calculate the term inside the parentheses:
$$ A = 750 \left(1 + \frac{0.05}{4}\right)^{4t} = 750 \left(1 + 0.0125\right)^{4t} = 750 (1.0125)^{4t} $$
Now, substituting ( t ) with 4:
$$ A = 750 (1.0125)^{16} $$
- Calculate the Final Balance
Now, we calculate ( (1.0125)^{16} ):
Using a calculator,
$$ (1.0125)^{16} \approx 1.221386025 $$
Therefore, we compute:
$$ A \approx 750 \times 1.221386025 \approx 915.99 $$
The balance of the account after 4 years is approximately $915.99.
More Information
This problem demonstrates how compound interest can significantly increase savings over time, especially with more frequent compounding periods. Understanding this can help in making informed savings decisions.
Tips
- Mistaking the formula for simple interest when compounding is involved.
- Not converting the interest rate to the correct form for compounding (decimals).
- Forgetting to correctly adjust the number of compounding periods when changing the time variable.
AI-generated content may contain errors. Please verify critical information