√(y³/x) × √(y/x)
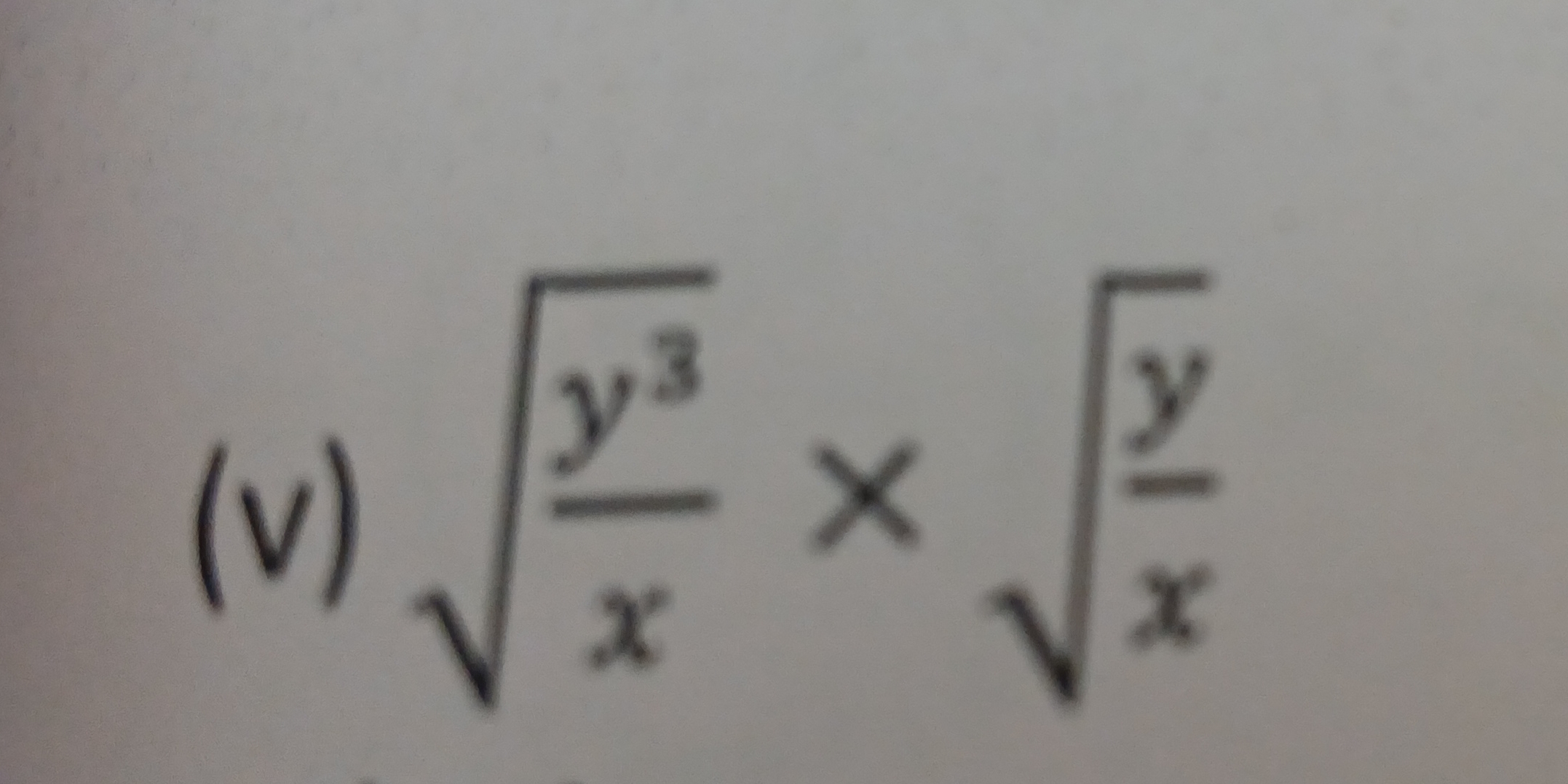
Understand the Problem
The question is presenting a mathematical expression that involves roots and requires simplification or multiplication. It seems to be asking for the outcome of the product of the square roots of certain variables.
Answer
The result is $\frac{y^2}{x}$.
Answer for screen readers
The final answer is $\frac{y^2}{x}$.
Steps to Solve
- Multiply the Square Roots We can use the property of square roots that states $\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}$. Applying this, we get:
$$ \sqrt{\frac{y^3}{x}} \times \sqrt{\frac{y}{x}} = \sqrt{\frac{y^3 \cdot y}{x \cdot x}} = \sqrt{\frac{y^4}{x^2}} $$
- Simplify the Resulting Square Root Now simplify the square root. We can separate the square root of the numerator and the denominator:
$$ \sqrt{\frac{y^4}{x^2}} = \frac{\sqrt{y^4}}{\sqrt{x^2}} $$
- Evaluate the Square Roots Now calculate the square roots of each term. Since $\sqrt{y^4} = y^2$ and $\sqrt{x^2} = x$, we have:
$$ \frac{\sqrt{y^4}}{\sqrt{x^2}} = \frac{y^2}{x} $$
The final answer is $\frac{y^2}{x}$.
More Information
This result shows how properties of square roots can simplify expressions involving powers and variables. It's useful in algebra for solving more complex equations and in calculus when dealing with limits and continuity.
Tips
- Confusing multiplication of square roots with addition. Remember to multiply the numbers inside the square root.
- Forgetting to simplify the resulting expression after combining the square roots. Always check if you can simplify further.
AI-generated content may contain errors. Please verify critical information