设二维随机变量(X, Y)的联合密度函数f(x, y)={21/4 * x^2 * y, 0 ≤ x^2 ≤ 1, 0 ≤ y ≤ 1; 其他地方为0},分别求X和Y的边际密度。
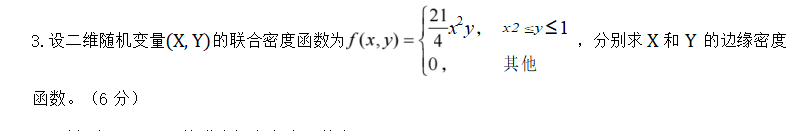
Understand the Problem
这个问题要求我们计算二维随机变量 (X, Y) 的联合概率密度函数 f(x, y) 的某些特征,特别是分求 X 和 Y 的边际密度。重点是理解给定的联合密度函数和其定义域。
Answer
- $f_X(x) = \frac{21}{8} x^2, \; 0 \leq x \leq 1$ - $f_Y(y) = \frac{7}{6} y, \; 0 \leq y \leq 1$
Answer for screen readers
边际密度函数为:
- $f_X(x) = \frac{21}{8} x^2, ; 0 \leq x \leq 1$
- $f_Y(y) = \frac{7}{6} y, ; 0 \leq y \leq 1$
Steps to Solve
- 定义边际密度函数 边际密度函数是通过对联合概率密度函数进行积分得到的。对于随机变量 $X$ 和 $Y$,其边际密度函数分别为:
- $f_X(x) = \int f(x, y) , dy$
- $f_Y(y) = \int f(x, y) , dx$
-
求 $X$ 的边际密度函数 根据给定的联合密度函数 $f(x, y)$,我们对 $y$ 从 $0$ 积分到 $1$: $$ f_X(x) = \int_0^1 f(x, y) , dy = \int_0^1 \left(\frac{21}{4} x^2 y\right) , dy $$ 计算积分: $$ f_X(x) = \frac{21}{4} x^2 \int_0^1 y , dy $$ $$ = \frac{21}{4} x^2 \cdot \left[\frac{y^2}{2}\right]_0^1 = \frac{21}{4} x^2 \cdot \frac{1}{2} = \frac{21}{8} x^2 $$ 注意范围是 $0 \leq x^2 \leq 1$。
-
求 $Y$ 的边际密度函数 同样,我们对 $x$ 从 $0$ 积分到 $1$,需要先写出 $f(x, y)$ 的表达式: $$ f_Y(y) = \int_{-\sqrt{1}}^{\sqrt{1}} f(x, y) , dx = \int_{-\sqrt{1}}^{\sqrt{1}} \left(\frac{21}{4} x^2 y\right) , dx $$ 积分计算: $$ f_Y(y) = \frac{21}{4} y \int_{-\sqrt{1}}^{\sqrt{1}} x^2 , dx $$ $$ = \frac{21}{4} y \cdot \left[\frac{x^3}{3}\right]_{-\sqrt{1}}^{\sqrt{1}} = \frac{21}{4} y \cdot \left(\frac{(1)^{3}}{3} - \frac{(-1)^{3}}{3}\right) $$ $$ = \frac{21}{4} y \cdot \left(\frac{1}{3} + \frac{1}{3}\right) = \frac{21}{4} y \cdot \frac{2}{3} = \frac{7}{6} y $$ 注意这里的范围是 $0 \leq y \leq 1$。
边际密度函数为:
- $f_X(x) = \frac{21}{8} x^2, ; 0 \leq x \leq 1$
- $f_Y(y) = \frac{7}{6} y, ; 0 \leq y \leq 1$
More Information
这些边际密度函数分别描述了随机变量 $X$ 和 $Y$ 在它们的定义域内的概率分布情况。计算边际密度函数的过程帮助了解到每个随机变量的独立行为。
Tips
- 在积分时忽略了变量的范围,可能会导致错误。
- 忘记了积分常数的正确选取,可能导致结果不一致。
AI-generated content may contain errors. Please verify critical information