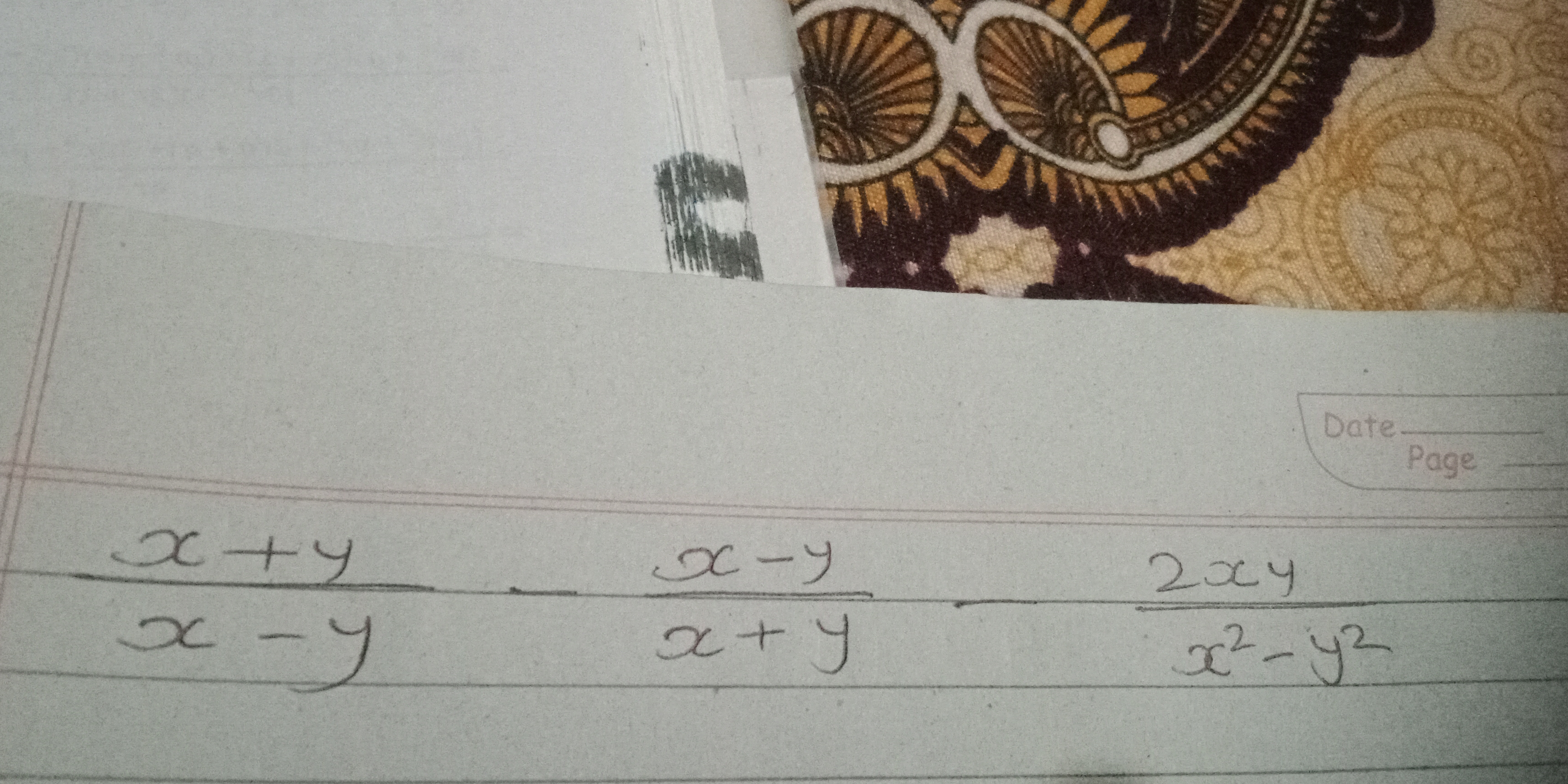
x + y / x - y; x - y / x + y; 2xy / x^2 - y^2
Understand the Problem
The question involves algebraic expressions that appear to be related to factoring or simplifying rational expressions. It might require performing operations like addition or subtraction of fractions based on the equations provided.
Answer
The final simplified expression is: $$ \frac{2(x^2 + y^2)}{(x - y)(x + y)} $$
Answer for screen readers
The final simplified expression is: $$ \frac{2(x^2 + y^2)}{(x - y)(x + y)} $$
Steps to Solve
-
Identify the Expression to Simplify The expression to simplify is: $$ \frac{x + y}{x - y} + \frac{x - y}{x + y} $$
-
Find a Common Denominator The common denominator for the fractions is $(x - y)(x + y)$. Rewrite each fraction: $$ \frac{(x + y)(x + y)}{(x - y)(x + y)} + \frac{(x - y)(x - y)}{(x - y)(x + y)} $$
-
Combine the Fractions Combine the fractions under the common denominator: $$ \frac{(x + y)^2 + (x - y)^2}{(x - y)(x + y)} $$
-
Expand the Numerator Expand $(x + y)^2$ and $(x - y)^2$: $$ (x + y)^2 = x^2 + 2xy + y^2 $$ $$ (x - y)^2 = x^2 - 2xy + y^2 $$ Now substitute back: $$ = \frac{(x^2 + 2xy + y^2) + (x^2 - 2xy + y^2)}{(x - y)(x + y)} $$
-
Simplify the Numerator Combine like terms: $$ = \frac{2x^2 + 2y^2}{(x - y)(x + y)} $$
-
Factor the Numerator Factor out the 2 from the numerator: $$ = \frac{2(x^2 + y^2)}{(x - y)(x + y)} $$
-
Final Simplified Expression The final expression after simplification is: $$ \frac{2(x^2 + y^2)}{(x - y)(x + y)} $$
The final simplified expression is: $$ \frac{2(x^2 + y^2)}{(x - y)(x + y)} $$
More Information
This problem demonstrates how to simplify rational expressions involving algebraic fractions by finding a common denominator, combining fractions, and performing algebraic expansion and factoring.
Tips
- Forgetting to find a common denominator can lead to incorrect results. Always ensure both fractions have the same denominator before combining.
- Not properly expanding the squares when combining terms can lead to mistakes in the final expression.
AI-generated content may contain errors. Please verify critical information