Write the function rule for g(x) in the form a(x - h)^2 + k.
Understand the Problem
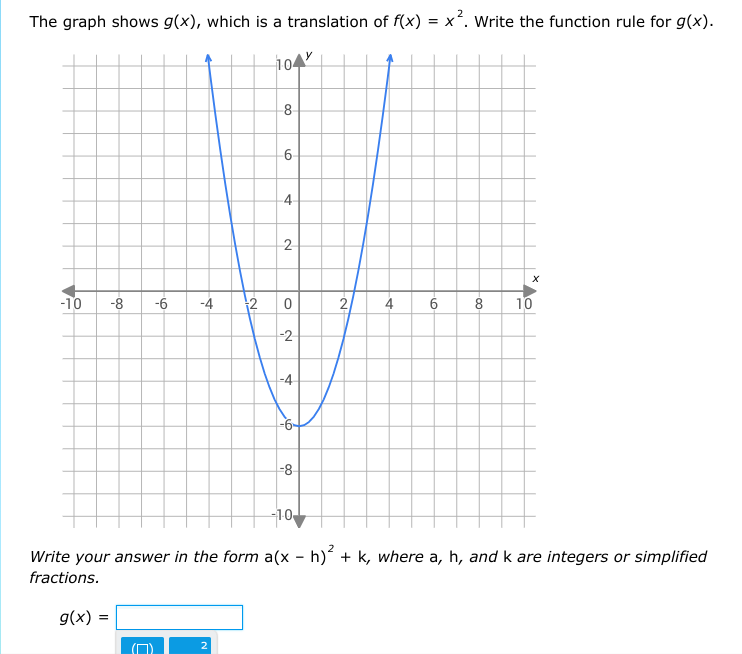
The question is asking us to write the function rule for g(x), which is a transformation of the quadratic function f(x) = x^2. We need to identify the values of a, h, and k that correspond to the graph shown in the image, which indicates translations and possibly reflections or stretches of the original function.
Answer
$$ g(x) = \frac{1}{4}x^2 - 6 $$
Answer for screen readers
The function rule is given by: $$ g(x) = \frac{1}{4}x^2 - 6 $$
Steps to Solve
-
Identify the Vertex of the Parabola From the graph, observe the vertex of the parabola. It appears to be at the point ( (0, -6) ).
-
Determine the Transformation Parameters The standard form of a quadratic function is given by ( g(x) = a(x - h)^2 + k ). Using the vertex, we have:
- ( h = 0 )
- ( k = -6 )
-
Analyze the Parabola's Direction The parabola opens upwards, indicating that ( a ) is positive. By selecting points on the graph, we can determine the value of ( a ). If we use the point ( (2, -5) ):
- Substitute into the equation: $$ -5 = a(2 - 0)^2 - 6 $$
- Simplifying: $$ -5 = 4a - 6 $$ $$ 4a = 1 $$ $$ a = \frac{1}{4} $$
-
Write the Function Rule Now that we have the values for ( a ), ( h ), and ( k ), we can write the function rule: $$ g(x) = \frac{1}{4}(x - 0)^2 - 6 $$
-
Simplify the function Simplifying gives: $$ g(x) = \frac{1}{4}x^2 - 6 $$
The function rule is given by: $$ g(x) = \frac{1}{4}x^2 - 6 $$
More Information
This function represents a parabola that has been translated vertically downward 6 units from the original position of the graph ( f(x) = x^2 ). The ( \frac{1}{4} ) factor indicates that the parabola is wider than the standard ( x^2 ) graph.
Tips
- Mistaking the direction of openness of the parabola; ensure to check if it opens upward or downward.
- Incorrectly calculating the value of ( a ) by not using the correct point on the graph.
AI-generated content may contain errors. Please verify critical information