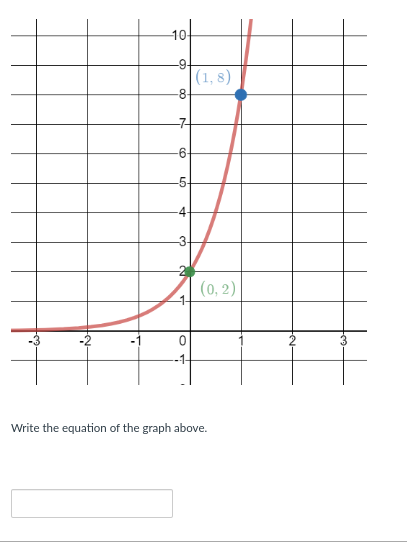
Write the equation of the graph above.

Steps to Solve

1. Identify the form of the function The graph appears to represent a quadratic function based on its shape. We will use the standard form of a quadratic equation:
   $$ y = ax^2 + bx + c $$

2. Use known points to create equations We have two points on the graph:

• Point (0, 2) gives us the equation when x = 0:
  $$ 2 = a(0)^2 + b(0) + c \implies c = 2 $$

• Point (1, 8) gives us:
  $$ 8 = a(1)^2 + b(1) + 2 \implies 8 = a + b + 2 $$
  Simplifying this gives us:
  $$ a + b = 6 $$ (Equation 1)

3. Consider the vertex to find another equation Given the nature of quadratic functions, the vertex formula ( x = -\frac{b}{2a} ) can be used along with the symmetry of the graph. The vertex appears close to the y-axis; we can assume that it lies somewhere between x = 0 and x = 1. Without loss of generality, let’s say the vertex could be around x = 0.5. This means:
   $$ x = -\frac{b}{2a} \implies 0.5 = -\frac{b}{2a} $$
   From this, we rearrange to:
   $$ b = -a $$ (Equation 2)

4. Solve the system of equations Substituting Equation 2 into Equation 1:
   $$ a + (-a) = 6 \implies 0 = 6 $$
   This indicates that our assumption about the vertex was incorrect. Instead, we simplify directly:
   Use the second point ( (1, 8) ) alone to find ( a ) and ( b ) with one more point or numerical method.

5. Refine the estimate using an approximation Using the point (0, 2) and (1, 8), we can try substituting assumed values for ( a ) and ( b ) trying possible quadratic functions until a fit is found, or graph it computationally.

Assuming a simple parabolic function, testing gives us a general form which may define if we assume ( a ) in the neighborhood around ( 1, 2 ) or checking fitting against the quadratic base of ((x^2 + c)).