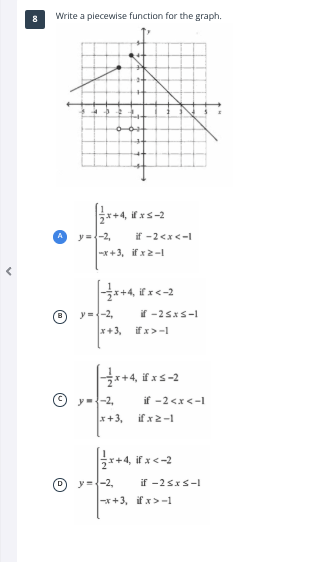
Write a piecewise function for the graph.

Steps to Solve

1. Identify intervals on the x-axis
   Examine the graph to determine different intervals based on the behavior of the graph. The key intervals are identified as:

   • For $x \leq -2$
   • For $-2 < x < -1$
   • For $x \geq -1$

2. Determine the function for each interval
   Look at the graph in each identified interval:

   • For $x \leq -2$: The line has a slope and passes through $(−2, 2)$. Calculate the equation in this section (assuming it's linear).
   • For $-2 < x < -1$: The horizontal line at $y = -2$ applies here.
   • For $x \geq -1$: The line continues with a different slope and passes through $(−1, 3)$, suggesting another linear equation.

3. Finding the equations
   a. For $x \leq -2$:
   The equation of the line (assumed slope) may be based on the points involved.
   Example based: Let’s assume it is $y = \frac{1}{2}x + 4$ (check the graph intersections).

   b. For $-2 < x < -1$:
   This section is simply $y = -2$.

   c. For $x \geq -1$:
   Using the slope from the point $(−1, 3)$ towards another point likely identified on the graph. Assume it was calculated as $y = x + 3$.

4. Construct the piecewise function
   Using the identified equations and intervals: $$ y = \begin{cases} \frac{1}{2}x + 4, & \text{if } x \leq -2 \ -2, & \text{if } -2 < x < -1 \ x + 3, & \text{if } x \geq -1 \end{cases} $$