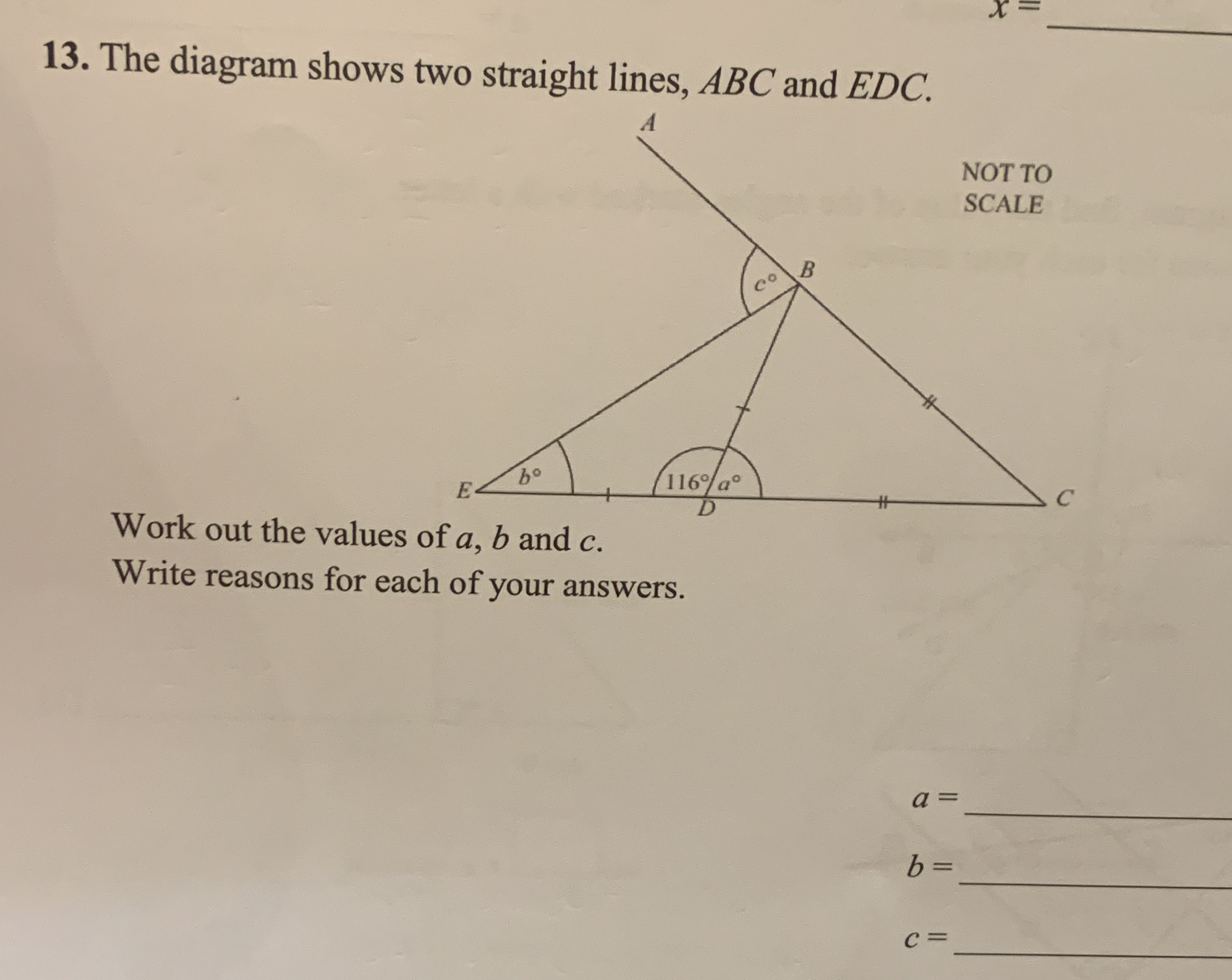
Work out the values of a, b and c. Write reasons for each of your answers.
Understand the Problem
The question is asking to calculate the values of angles a, b, and c in the given diagram, and to provide reasons for each of the answers based on the properties of angles in lines and triangles.
Answer
$a = 32^\circ$, $b = 116^\circ$, $c = 32^\circ$
Answer for screen readers
$a = 32^\circ$
$b = 116^\circ$
$c = 32^\circ$
Steps to Solve
- Calculate angle c
In triangle EDC, the angles sum to 180°. We know angle E is $a^\circ$ and angle C is given as $116^\circ$. Hence, we can find angle D:
$$ c = 180^\circ - a - 116^\circ $$
- Identify angle a
Since angle A and angle B are vertically opposite angles, they are equal. Therefore, we have:
$$ a = c $$
So now we can rewrite the equation for angle c:
$$ c = 180^\circ - c - 116^\circ $$
- Set up the equation for angle a
Substituting in angle c gives us:
$$ 2c = 64^\circ $$
Then dividing by 2:
$$ c = 32^\circ $$
Thus:
$$ a = 32^\circ $$
- Calculate angle b
In triangle ABC, we now know angles A and C. To find angle B, we again use the sum of angles in a triangle:
$$ b = 180^\circ - a - c $$
Now substituting in our values:
$$ b = 180^\circ - 32^\circ - 32^\circ = 116^\circ $$
$a = 32^\circ$
$b = 116^\circ$
$c = 32^\circ$
More Information
In this problem, we utilized the properties of triangles, where the sum of the angles is always 180°. We also used the fact that vertically opposite angles are equal.
Tips
- Miscalculating the sum of angles in triangles: Remember each triangle must add up to exactly 180°.
- Confusing vertically opposite angles: It's important to remember that these angles are always equal.
AI-generated content may contain errors. Please verify critical information