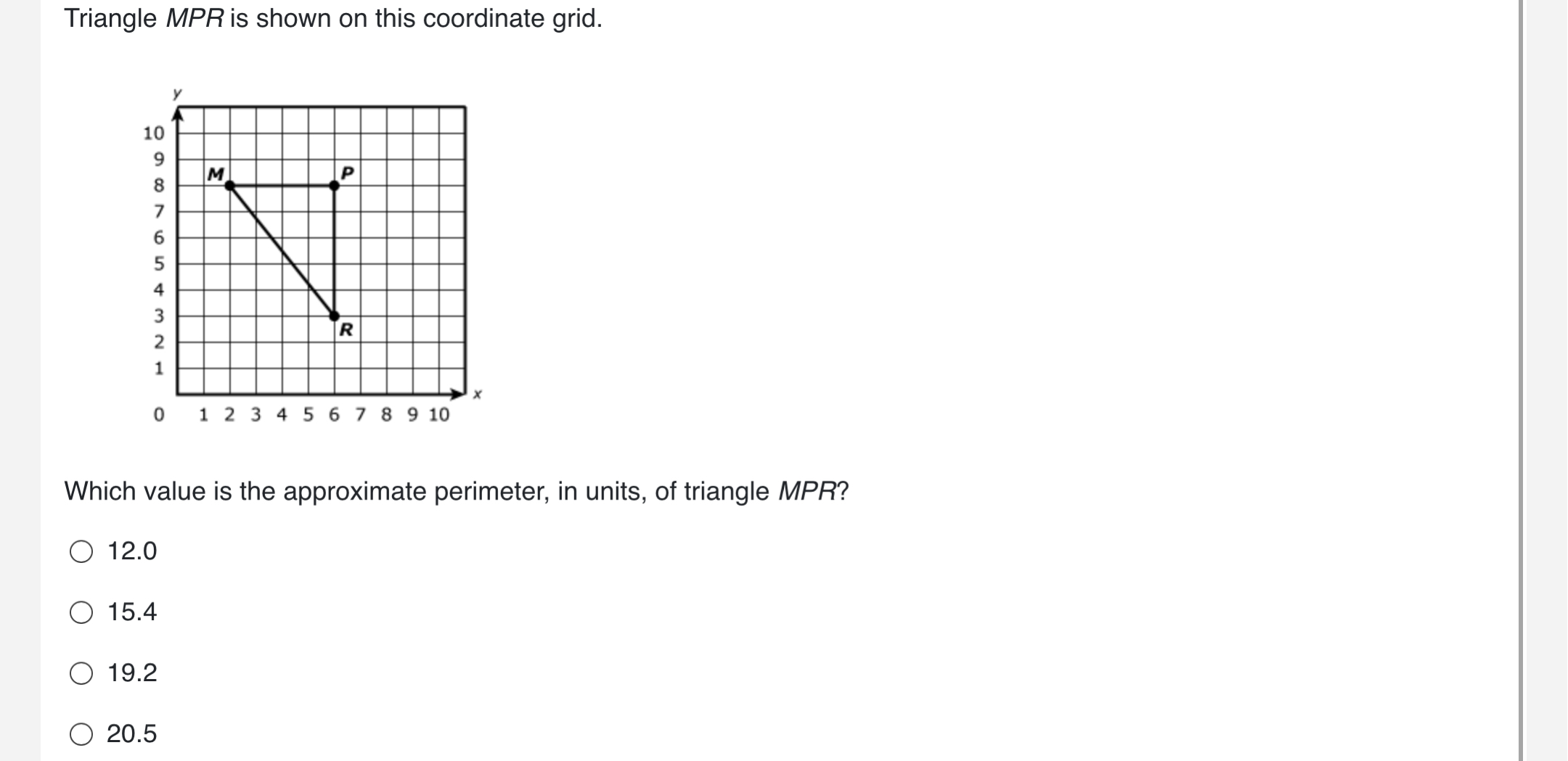
Which value is the approximate perimeter, in units, of triangle MPR?
Understand the Problem
The question is asking for the calculation of the approximate perimeter of triangle MPR, which is represented on a coordinate grid. To find the perimeter, we need to determine the lengths of the sides of the triangle using their coordinates and then sum these lengths.
Answer
$12$
Answer for screen readers
The approximate perimeter of triangle MPR is $12$ units.
Steps to Solve
-
Identify the Coordinates of Points M, P, and R
From the graph, the coordinates are as follows:
- Point $M(3, 8)$
- Point $P(3, 5)$
- Point $R(7, 5)$
-
Calculate the Length of Side MP
Since points M and P have the same x-coordinate, the length of side $MP$ can be found by subtracting the y-coordinates: [ MP = |y_M - y_P| = |8 - 5| = 3 ]
-
Calculate the Length of Side PR
Since points P and R have the same y-coordinate, the length of side $PR$ can be found by subtracting the x-coordinates: [ PR = |x_R - x_P| = |7 - 3| = 4 ]
-
Calculate the Length of Side RM
To calculate the length of side $RM$, use the distance formula: [ RM = \sqrt{(x_R - x_M)^2 + (y_R - y_M)^2} ]
Substituting the values: [ RM = \sqrt{(7 - 3)^2 + (5 - 8)^2} = \sqrt{4^2 + (-3)^2} = \sqrt{16 + 9} = \sqrt{25} = 5 ]
-
Calculate the Perimeter of Triangle MPR
The perimeter $P$ is the sum of all sides: [ P = MP + PR + RM = 3 + 4 + 5 = 12 ]
The approximate perimeter of triangle MPR is $12$ units.
More Information
The perimeter is the total distance around a triangle, which can be calculated by summing the lengths of its sides. In this scenario, the coordinates of the triangle vertices were utilized to find these lengths.
Tips
- Forgetting to use the correct formula for distance, especially when dealing with vertical and horizontal lines.
- Confusing x-coordinates and y-coordinates during calculations.
AI-generated content may contain errors. Please verify critical information