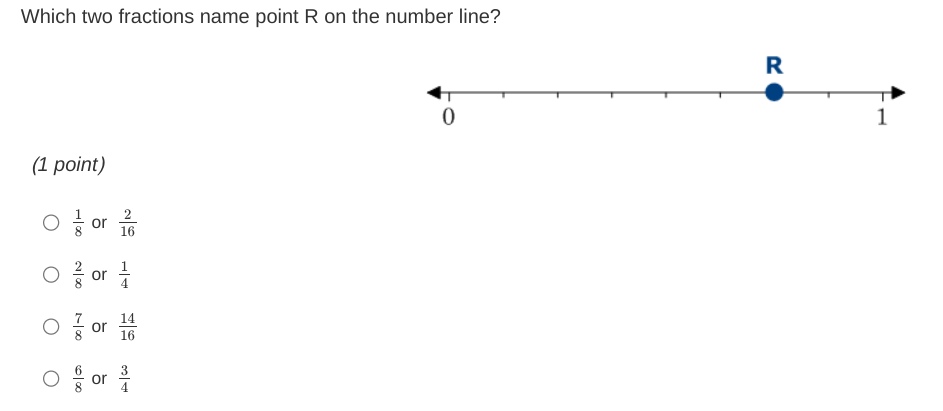
Which two fractions name point R on the number line?

Steps to Solve

1. Identify the Position of R on the Number Line

The point R is between 0 and 1. By estimating its position, we can say it's around the halfway mark.

2. Convert Fractions to Decimal Form for Comparison

Convert each fraction provided in the options into decimal form for easier comparison:

• $ \frac{1}{8} = 0.125 $
• $ \frac{2}{16} = 0.125 $
• $ \frac{2}{8} = 0.25 $
• $ \frac{1}{4} = 0.25 $
• $ \frac{7}{8} = 0.875 $
• $ \frac{14}{16} = 0.875 $
• $ \frac{6}{8} = 0.75 $
• $ \frac{3}{4} = 0.75 $

3. Locate Possible Options on the Number Line

Identify which decimal values are close to 0.5:

• $0.125$ (from $ \frac{1}{8}$ and $ \frac{2}{16}$)
• $0.25$ (from $ \frac{2}{8}$ and $ \frac{1}{4}$)
• $0.875$ (from $ \frac{7}{8}$ and $ \frac{14}{16}$)
• $0.75$ (from $ \frac{6}{8}$ and $ \frac{3}{4}$)

Since the position of R is approximately 0.5, it is clear that none of those options are suitable.

4. Reviewing Results and Choosing the Correct Fractions

Reassess which of the fractions adequately reflects the R point's approximate location. Since 0.5 is represented by $ \frac{2}{4} = \frac{1}{2} $, none of the listed fractions correspond exactly to this.

However, when we look closely, from the fractions provided, we note $ \frac{2}{8} = 0.25$ is closest to the left, and $ \frac{7}{8} = 0.875$ is positioned towards the right.