Prove that cosh^2(θ) - sinh^2(θ) = 1
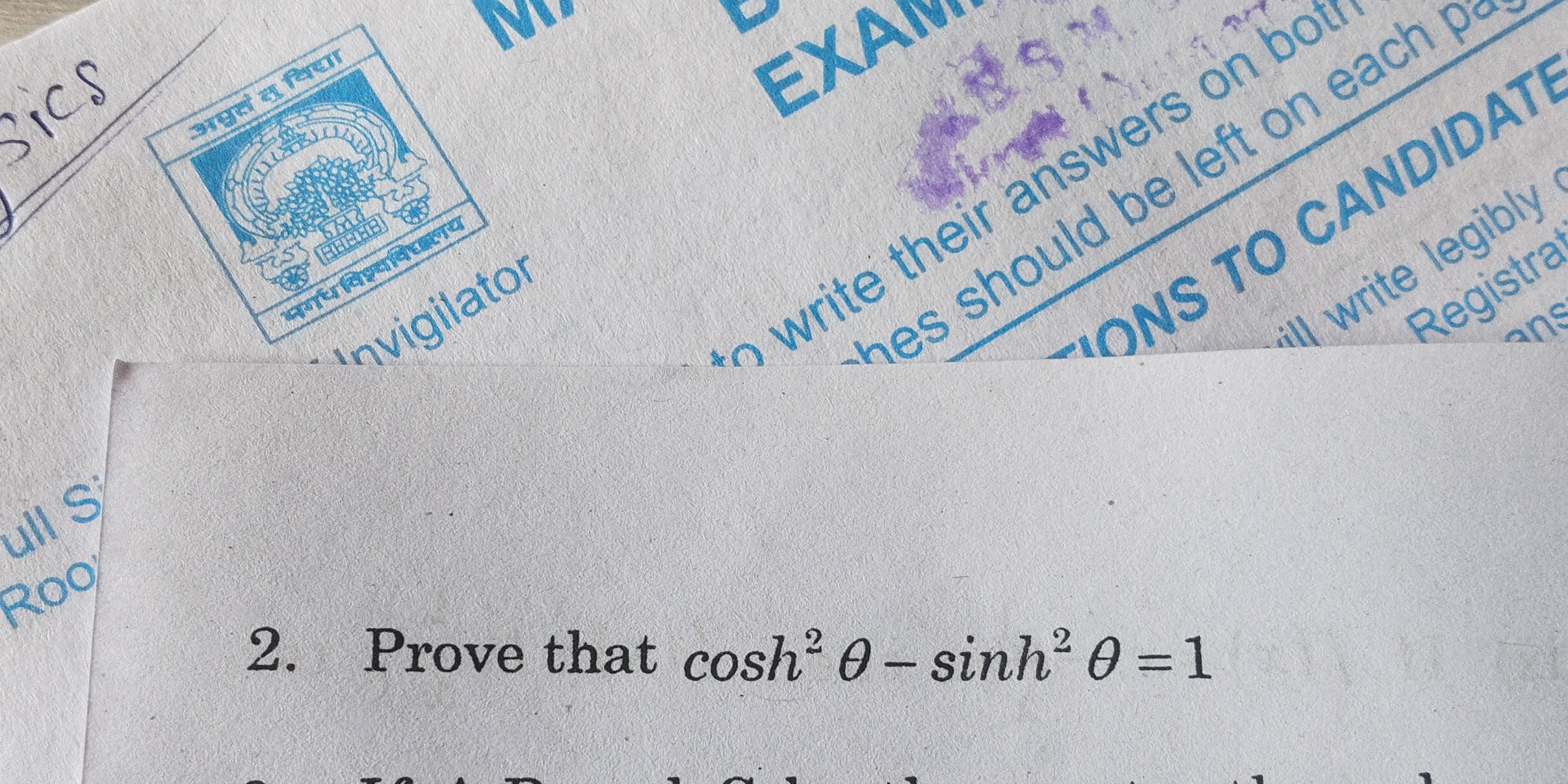
Understand the Problem
The question asks to prove the hyperbolic trigonometric identity (\cosh^2(\theta) - \sinh^2(\theta) = 1). This involves demonstrating that the difference between the square of the hyperbolic cosine and the square of the hyperbolic sine of an angle (\theta) is equal to 1. We need to show how to derive this result using the definitions of (\cosh(\theta)) and (\sinh(\theta)).
Answer
$\cosh^2 \theta - \sinh^2 \theta = 1$
Answer for screen readers
$\cosh^2 \theta - \sinh^2 \theta = 1$
Steps to Solve
- Define $\cosh \theta$ and $\sinh \theta$
Recall the definitions of hyperbolic cosine and hyperbolic sine: $$ \cosh \theta = \frac{e^\theta + e^{-\theta}}{2} $$ $$ \sinh \theta = \frac{e^\theta - e^{-\theta}}{2} $$
- Compute $\cosh^2 \theta$ and $\sinh^2 \theta$
Square both definitions: $$ \cosh^2 \theta = \left( \frac{e^\theta + e^{-\theta}}{2} \right)^2 = \frac{e^{2\theta} + 2e^\theta e^{-\theta} + e^{-2\theta}}{4} = \frac{e^{2\theta} + 2 + e^{-2\theta}}{4} $$ $$ \sinh^2 \theta = \left( \frac{e^\theta - e^{-\theta}}{2} \right)^2 = \frac{e^{2\theta} - 2e^\theta e^{-\theta} + e^{-2\theta}}{4} = \frac{e^{2\theta} - 2 + e^{-2\theta}}{4} $$
- Compute $\cosh^2 \theta - \sinh^2 \theta$
Subtract $\sinh^2 \theta$ from $\cosh^2 \theta$: $$ \cosh^2 \theta - \sinh^2 \theta = \frac{e^{2\theta} + 2 + e^{-2\theta}}{4} - \frac{e^{2\theta} - 2 + e^{-2\theta}}{4} $$ $$ = \frac{(e^{2\theta} + 2 + e^{-2\theta}) - (e^{2\theta} - 2 + e^{-2\theta})}{4} $$ $$ = \frac{e^{2\theta} + 2 + e^{-2\theta} - e^{2\theta} + 2 - e^{-2\theta}}{4} $$ $$ = \frac{4}{4} = 1 $$
$\cosh^2 \theta - \sinh^2 \theta = 1$
More Information
This identity is analogous to the trigonometric identity $\cos^2 \theta + \sin^2 \theta = 1$.
Tips
A common mistake is in the expansion of the squares of $\cosh \theta$ and $\sinh \theta$, specifically with the sign of the cross term: $$ (e^\theta - e^{-\theta})^2 = e^{2\theta} - 2 + e^{-2\theta}. $$ Another common mistake is not simplifying $e^\theta e^{-\theta}$ to 1.
AI-generated content may contain errors. Please verify critical information