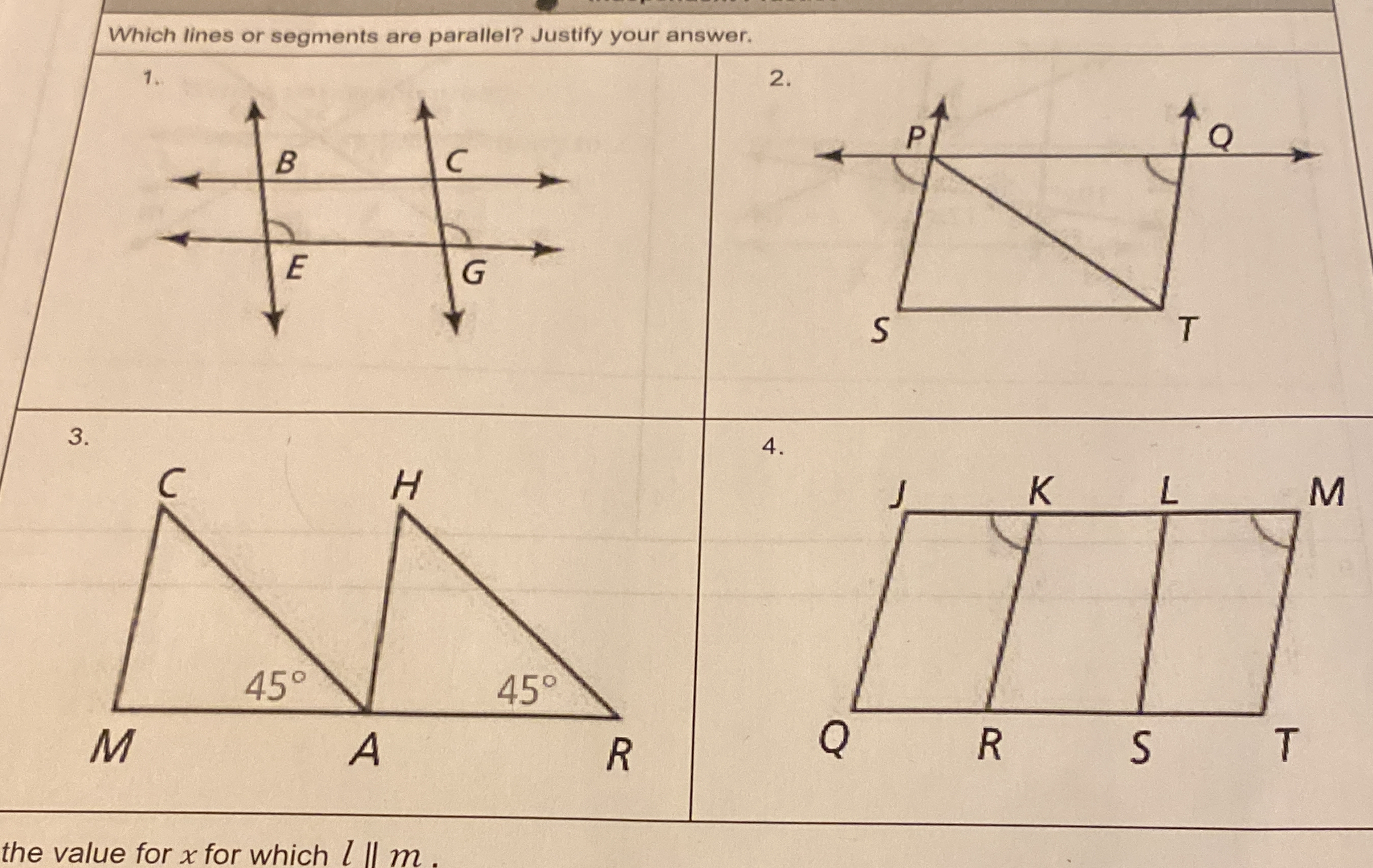
Which lines or segments are parallel? Justify your answer.
Understand the Problem
The question involves identifying which lines or segments are parallel in the provided images and requires justification for the answer. It presents multiple geometric diagrams, and the task is to analyze each diagram to determine parallel lines and provide reasoning based on the properties of angles, lines, and shapes.
Answer
1. $B \parallel C$ 2. $P \parallel Q$ 3. $CM \parallel HR$ 4. $QR \parallel RS \parallel ST$
Answer for screen readers
-
Lines $B$ and $C$ are parallel: $B \parallel C$.
-
Lines $P$ and $Q$ are parallel: $P \parallel Q$.
-
Lines $CM$ and $HR$ are parallel: $CM \parallel HR$.
-
Lines $QR$, $RS$, and $ST$ are parallel: $QR \parallel RS \parallel ST$.
Steps to Solve
- Identify Parallel Lines in Diagram 1
Lines $B$ and $C$ are parallel because they are cut by transversal $E$, and the corresponding angles formed ($\angle BEG$ and $\angle CEG$) are equal. Thus, $B \parallel C$.
- Identify Parallel Lines in Diagram 2
Lines $P$ and $Q$ are parallel because they are both horizontal, and lines $S$ and $T$ act as a transversal. The angles formed at intersections with the transversal are equal ($\angle PSQ$ and its corresponding angle).
- Identify Parallel Lines in Diagram 3
Triangles $MCA$ and $HRA$ show that the angles near $A$ are both $45^\circ$. Since these are alternate interior angles when comparing the line $CR$ and the extensions of angles at $A$, then line segment $C$ is parallel to $H$. Thus, $CM \parallel HR$.
- Identify Parallel Lines in Diagram 4
Rectangles in diagram four indicate that lines $QR$, $RS$, and $ST$ are all parallel because they are opposite sides of the rectangles. The angles at points $J$ and $M$ are equal as alternate interior angles, confirming parallelism.
-
Lines $B$ and $C$ are parallel: $B \parallel C$.
-
Lines $P$ and $Q$ are parallel: $P \parallel Q$.
-
Lines $CM$ and $HR$ are parallel: $CM \parallel HR$.
-
Lines $QR$, $RS$, and $ST$ are parallel: $QR \parallel RS \parallel ST$.
More Information
Understanding parallel lines is crucial in geometry, as they maintain consistent distances apart and do not meet. The study of angles and how they relate when a transversal crosses parallel lines can help identify these relationships.
Tips
- Confusing corresponding angles with alternate interior angles; always check their positions.
- Not recognizing that straight lines and their extensions are also considered when determining parallelism.
AI-generated content may contain errors. Please verify critical information