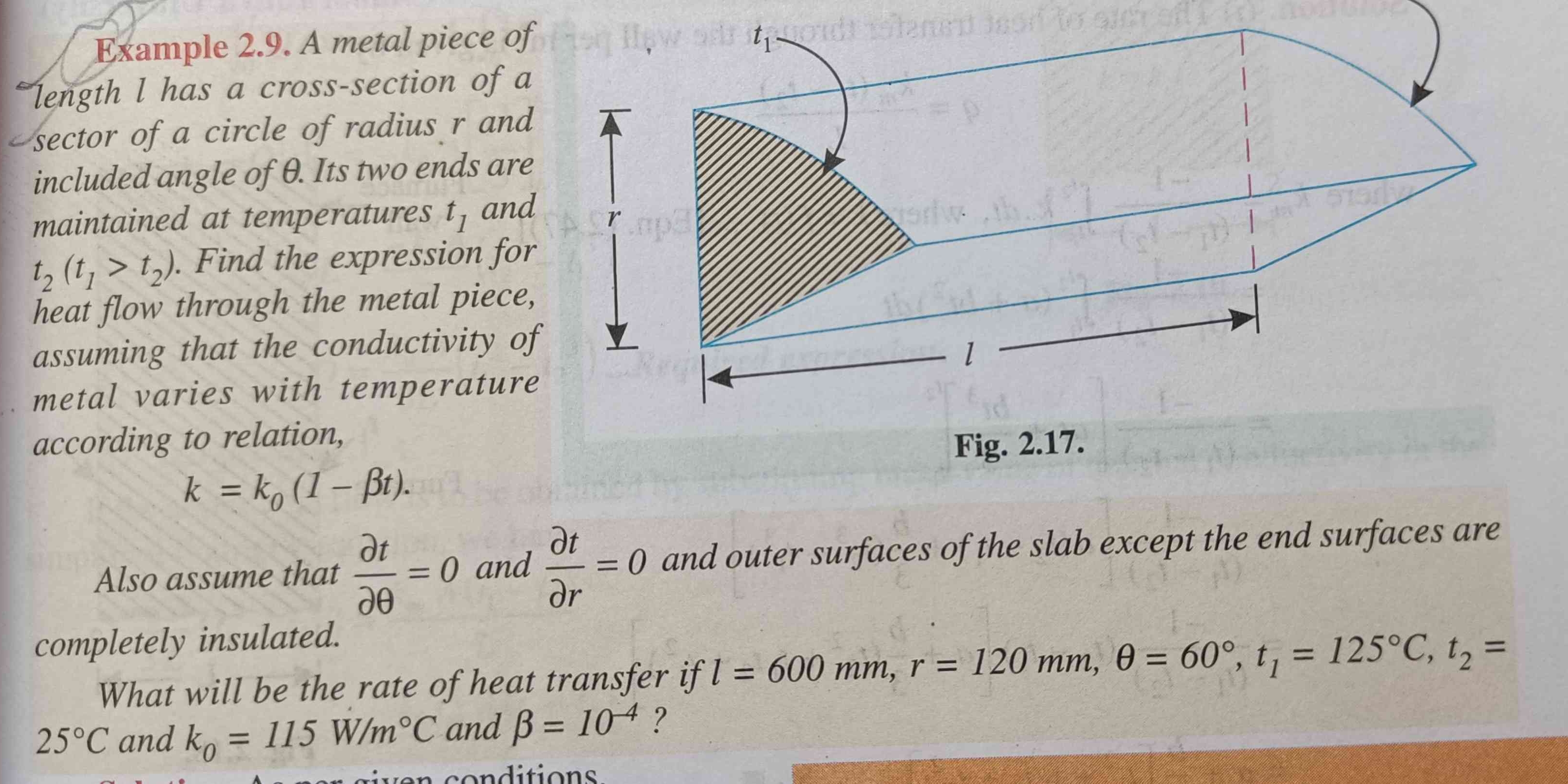
What will be the rate of heat transfer if l = 600 mm, r = 120 mm, θ = 60°, t1 = 125°C, t2 = 25°C and k0 = 115 W/m°C and β = 10^-4?

Steps to Solve

1. Understanding the Heat Transfer Equation

The rate of heat transfer through a material can be derived from Fourier's law of heat conduction. For a cylindrical geometry, the equation is given as:

$$ Q = -k \cdot A \cdot \frac{dT}{dx} $$

where $Q$ is heat transfer rate, $k$ is thermal conductivity, $A$ is the area through which heat is being transferred, and $\frac{dT}{dx}$ is the temperature gradient.

2. Expressing Area in Terms of Geometry

The area $A$ for a cylindrical piece with an included angle $\theta$ can be calculated as:

$$ A = \frac{1}{2} \cdot r^2 \cdot \theta $$

3. Incorporating Temperature-Dependent Conductivity

Given that the thermal conductivity $k$ varies with temperature as:

$$ k = k_0(1 - \beta T) $$

we need to express this in terms of the average temperature. The average temperature, $T_{avg}$, can be approximated as:

$$ T_{avg} = \frac{t_1 + t_2}{2} $$

4. Setting Up the Integral for Heat Transfer

Since $k$ varies with temperature, heat transfer will require integration over the temperature gradient:

$$ Q = -\int_{t_2}^{t_1} k \cdot \frac{A}{l} dT $$

5. Calculating the Heat Transfer Rate

From the above integral, express $Q$ as:

$$ Q = -\int_{t_2}^{t_1} k_0(1 - \beta T) \cdot \frac{\frac{1}{2} r^2 \theta}{l} dT $$

Evaluating this integral gives:

$$ Q = \frac{1}{2} \cdot \frac{r^2 \theta}{l} \cdot \left[ k_0 (t_1 - t_2) - \frac{k_0 \beta}{2} (t_1^2 - t_2^2) \right] $$

6. Substituting Given Values to Calculate Q

Substitute the given parameters into the expression:

• $l = 600 \text{ mm} = 0.6 \text{ m}$
• $r = 120 \text{ mm} = 0.12 \text{ m}$
• $\theta = 60^\circ = \frac{\pi}{3} \text{ radians}$
• $t_1 = 125^\circ C$, $t_2 = 25^\circ C$
• $k_0 = 115 \text{ W/m°C}$ and $\beta = 10^{-4} \text{ }$

After substituting the values, calculate $Q$.