What value of b makes the equation true? 5 (5 - 3b) = -20 - 6b
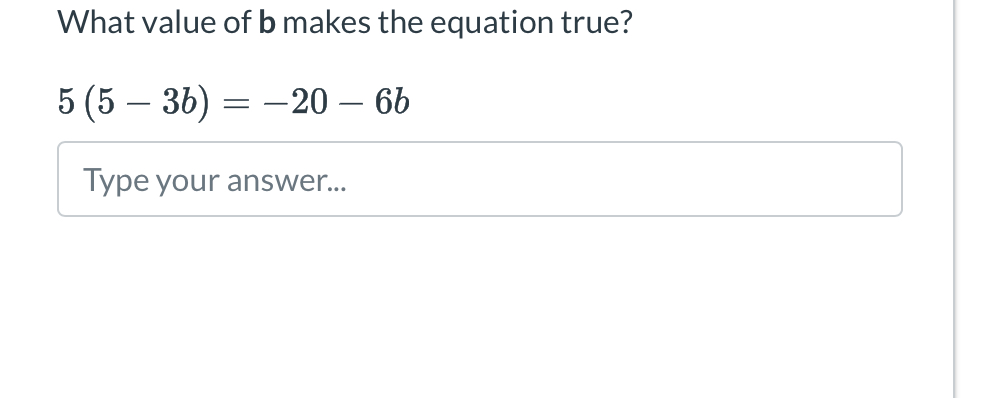
Understand the Problem
The question is asking for the value of b that satisfies the given equation. We need to solve the equation by simplifying both sides and isolating b.
Answer
The value of \( b \) is \( 5 \).
Answer for screen readers
The value of ( b ) that makes the equation true is ( b = 5 ).
Steps to Solve
- Distribute on the left side
Distributing the $5$ through the parentheses in $5(5 - 3b)$:
$$ 5 \cdot 5 - 5 \cdot 3b = 25 - 15b $$
- Set the equation
Now we rewrite the equation with the distributed terms:
$$ 25 - 15b = -20 - 6b $$
- Isolate terms involving b
Add $15b$ to both sides to move the $b$ terms to one side:
$$ 25 = -20 + 9b $$
- Add 20 to both sides
We can add $20$ to both sides to isolate the constant term:
$$ 25 + 20 = 9b $$
This simplifies to:
$$ 45 = 9b $$
- Solve for b
Divide both sides by $9$ to find $b$:
$$ b = \frac{45}{9} = 5 $$
The value of ( b ) that makes the equation true is ( b = 5 ).
More Information
The equation we solved is a linear equation. Solving for ( b ) often involves distributing terms and isolating the variable. Here, we distributed to eliminate parentheses and combined like terms.
Tips
- Not distributing correctly: A common mistake is misapplying the distributive property. Always ensure that each term inside the parentheses is multiplied correctly.
- Forgetting to combine like terms: Make sure to collect terms involving ( b ) on one side of the equation to simplify solving it.
AI-generated content may contain errors. Please verify critical information