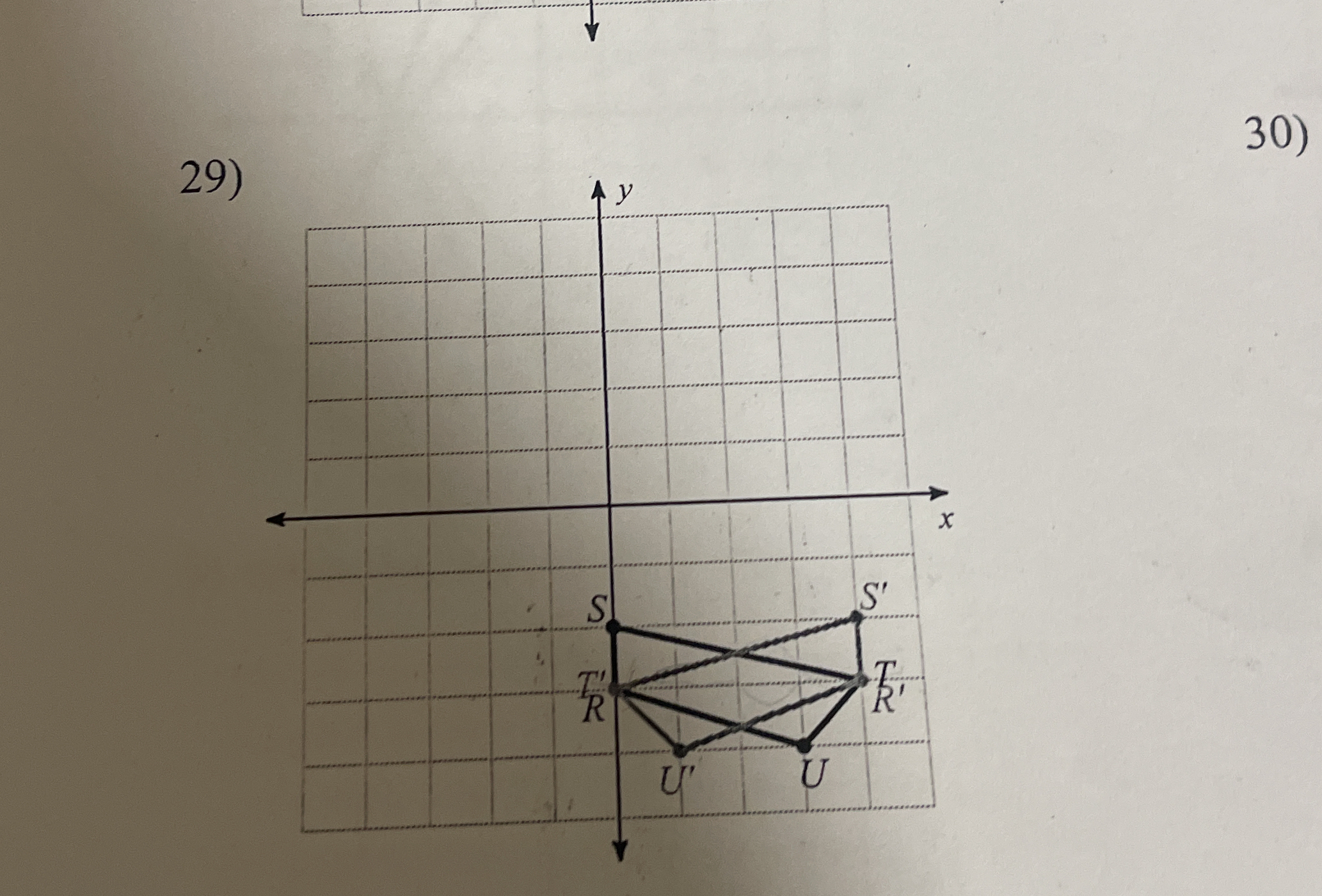
What type of geometric transformation is represented by the given figure?
Understand the Problem
The question involves analyzing a geometric transformation represented by a figure on a coordinate grid. It likely requires identifying the type of transformation or demonstrating the properties of the shapes involved.
Answer
The transformation is a reflection.
Answer for screen readers
The geometric transformation is likely a reflection, as the points ( S, T, R, U ) and ( S', T', R', U' ) appear symmetric about a horizontal line in the coordinate plane.
Steps to Solve
-
Identify the Points of the Figures
The original figure has points: ( S, T, R, U ) and the transformed figure has points: ( S', T', R', U' ). Note their coordinates.
-
Determine the Transformation
By comparing the original and transformed points, determine the type of geometric transformation involved (e.g., translation, reflection, rotation).
-
Calculate Coordinate Changes
For each point, calculate how the coordinates changed. For instance, if ( S(1, 2) ) transformed to ( S'(1, 4) ), note the change in the ( y )-coordinate.
-
Verify Transformation Type
If the transformation is a translation, all points should shift uniformly in one direction. If it’s a reflection, check symmetry about a line. For a rotation, calculate the angle of rotation.
-
Analyze Properties
Identify properties like congruence or similarity. For instance, determine if segments between corresponding points are equal in length or if angles remain unchanged.
The geometric transformation is likely a reflection, as the points ( S, T, R, U ) and ( S', T', R', U' ) appear symmetric about a horizontal line in the coordinate plane.
More Information
This reflects the basic principles of geometric transformations, showing how shapes can be manipulated while maintaining certain properties such as congruence and symmetry. Understanding these transformations is foundational in geometry.
Tips
- Misidentifying the transformation type by not thoroughly comparing points.
- Overlooking changes in angles or distances that determine similarity or congruency.
- Forgetting to calculate the changes in coordinates accurately.
AI-generated content may contain errors. Please verify critical information